Parallélogrammes

Parallélogrammes
Définition 1 :
Un quadrilatère est un parallélogramme si et seulement si ses côtés opposés sont parallèles 2 à 2.
ABCD parallélogramme ñ (AB)//(CD) et (AD)//(BC)
Propriétés du parallélogramme
Dans un parallélogramme ABCD :
 Les côtés opposés sont parallèles 2 à 2 : (AB)//(CD) et (AD)//(BC)
 Les côtés opposés ont égaux 2 à 2 : AB= CD et AD = BC
 les angles opposés sont égaux 2 à 2 :
A= C
et
B= D
 Les diagonales ont le même milieu : Les segments [AC] et [BD] ont le même milieu.
AB= DC
et
AD= BC
 Le point d'intersection des diagonales est centre de symétrie du parallélogramme.
Propriétés caractéristiques
Pour démontrer qu'un quadrilatère est un parallélogramme, il suffit d'utiliser l'une des propriétés
P1 : (AB)//(CD) et (AD)//(BC) ñ ABCD parallélogramme
P2 : [AC] et [BD] ont le même milieu ñ ABCD parallélogramme
P3 :
AB= DC
ñ ABCD parallélogramme
P4 :
AD= BC
ñ ABCD parallélogramme
Si le quadrilatère ABCD est non croisé
P5 : AB= CD et AD = BC ñ ABCD parallélogramme
P6 :
A= C
et
B= D
ñ ABCD parallélogramme
P7 : AB= CD et (AB)//(CD) ñ ABCD parallélogramme
1/2

Parallélogrammes particuliers
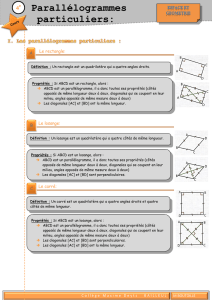
Rectangle
Définition :
Un rectangle est un quadrilatère dont les quatres angles sont droits.
Propriétés du rectangle :
Un rectangle est un parallélogramme particulier, il en possède donc toutes les propriétés.
En plus, il possède les propriétés suivantes :
 Les angles sont droits.
 Les diagonales sont de la même longueur.
 Les médiatrices des côtés sont des axes de symétrie du rectangle.
Pour démontrer qu'un parallélogramme est un rectangle, il suffit d'utiliser l'une des
propriétés suivantes :
R1 : Un rectangle est un parallélogramme qui possède un angle droit.
R2 : Un rectangle est un parallélogramme dont les diagonales ont la même longueur.
Losange
Définition :
Un losange est un quadrilatère dont les quatres côtés ont la même longueur.
Propriétés du losange :
Un losange est un parallélogramme particulier, il en possède donc toutes les propriétés.
En plus, il possède les propriétés suivantes :
 Les quatre côtés sont de la même longueur .
 Les diagonales sont perpendiculaires.
 les diagonales sont des axes de symétrie du losange.
Pour démontrer qu'un parallélogramme est un losange, il suffit d'utiliser l'une des
propriétés suivantes :
L1 : Un losange est un parallélogramme qui possède deux côtés consécutifs de même longueur.
L2 : Un losange est un parallélogramme dont les diagonales sont perpendiculaires.
Carré
Définition
Un carré est un quadrilatère qui a quatre angles droits et les quatre côtés de la même longueur.
Propriétés
Un carré est à la fois un rectangle et un losange, il possède donc toutes les propriétés du rectangle
et toutes les propriétés du losange.
Pour démontrer qu'un parallélogramme est un carré, il suffit d'utiliser l'une des
propriétés du rectangle ( R1 ou R2) et l'une des propriétés du losange ( L1 ou L2).
2/2