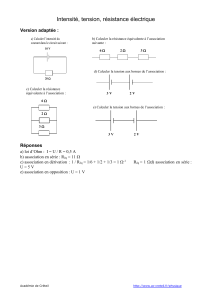
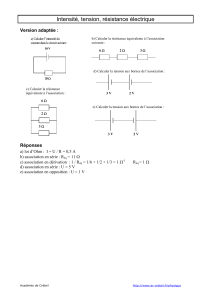
circuit v -b

1
Rappel : Préparation pour l ’examen de laboratoire
Labo 1 : Initiation aux circuits
+
–
a
A
Courant dans l’ampoule
+
–
S
i 1= ± mA
i 1= mA± %
Verte
- Monter et schématiser quelques circuits électriques.
- Observer le comportement du filament métallique d’une ampoule
électrique en fonction des variations du courant électrique.
- Utiliser adéquatement un multimètre numérique.
- Évaluer l’incertitude sur la lecture à l’aide du multimètre.
Chapitre 6 , 6.1
-
- +
+

2
Étude de la résistance électrique, de son effet sur l’intensité du courant et
sur la puissance électrique fournie à un élément
Buts
• Mesurer correctement une résistance au carbone par 3 méthodes
différentes.
• Mesurer la tension aux bornes de résistances ainsi que l’intensité du
courant qui les traverse.
• Calculer la puissance dissipée en chaleur.
• Vérifier les lois d’association de résistances branchées en série
et en parallèle.
• Vérifier la loi d’Ohm dans le cas d’une résistance au carbone et
d’une ampoule.
Labo 2 : Étude de la résistance électrique

3
3 méthodes
Le codes des couleurs
L’ohmmètre numérique
Mesure de V et I
+
–
+
–
V
S
ε
R
i
A
∆V
– +
– +

4
Rappel : Préparation pour l ’examen de laboratoire
∆ V
I I
v v v
E
R
V
I∆ =
En appliquant une différence
de potentiel, on sait
expérience que I sera donné
par
Puisque dans le fil,
ELV=∆
C’est le champ électrique qui
pousse les charges libres
dans le fil
Labo : Étude de la résistance
Chapitre 6, Sections 6.1 et 6.2
Calculer correctement une résistance et vérifier les lois d’association

5
Rappel : Préparation pour l ’examen de laboratoire
R
V
I∆ =
•La différence de potentiel de la pile fournit de l’énergie électrique aux
charges électriques. Ces charges perdent cette l’énergie électrique en
parcourant le circuit jusqu’à leur retour la borne négative de la pile. En
parcourant le circuit, les charges transmettent cette énergie aux différents
éléments du circuit.
En chaque
point
∆U = q∆V
∆V
∆ V
I I
v v v
t
q
I∆
∆
=
q
q
q
+ -
Chapitre 6, Section 6.3