1 Existence d`un champ d`interférences 2 Description de la figure d

MP1 Lycée Janson de Sailly DM n°13
DM n°13
Pour le mardi 21 février 2017
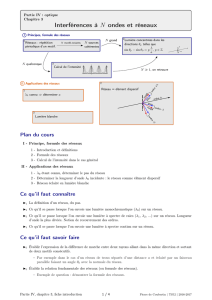
On réalise, dans l’air, l’expérience des trous d’Young à l’aide du
dispositif décrit et schématisé ci-dessous. Un laser, de longueur d’onde
dans le vide λ, émet un faisceau lumineux cylindrique d’axe z0z.
On suppose par la suite que le faisceau du laser éclaire entière-
ment et de manière uniforme les différentes ouvertures qui sont pla-
cées sur son passage. Ce faisceau est constitué de rayons parallèles
qui semblent provenir d’une source ponctuelle Ssituée à l’infini.
Une plaque opaque (P), percée de deux trous circulaires S1et S2de
même taille et de faibles dimensions, est placée perpendiculairement
à l’axe z0z. On note O0le milieu du segment [S1S2]. Le point O0
appartient à l’axe z0z. La distance entre les centres des deux trous
S1et S2est notée a.
Le phénomène d’interférences est observé sur un écran (E)placé
perpendiculairement à l’axe z0z. Soit Ole point de l’écran (E)appar-
tenant à l’axe z0z. La distance entre la plaque (P)et l’écran (E)est
égale à D. On a ainsi D=O0O.
L’espace est rapporté au repère cartésien (O, ~ex, ~ey, ~ez)défini
comme suit :
? ~ez: vecteur unitaire de l’axe Oz, orienté de la plaque (P)vers
l’écran (E).
? ~ex: vecteur unitaire de l’axe Ox, parallèle à −−→ S1S2et orienté de
S2vers S1.
? ~ey: vecteur unitaire de l’axe Oy tel que la base (~ex, ~ey, ~ez)soit
orthonormée directe.
Dans tout le problème, l’indice de réfraction de l’air sera pris égal
à 1.
Figure 1 –
1 Existence d’un champ d’interférences
1. En se référant uniquement aux lois de l’optique géométrique,
quelle devrait être l’allure de la figure observée sur l’écran (E) ?
2. Pour quelle raison l’optique géométrique ne permet-elle pas de
prévoir l’existence d’un champ d’interférences dans le cas du dis-
positif des trous d’Young ? À quel phénomène physique doit-on
faire appel pour en comprendre l’existence ?
2 Description de la figure d’interférences
Les réponses aux questions suivantes seront justifiées. Une démons-
tration quantitative ne sera toutefois pas exigée.
1. Qu’observe-t-on sur l’écran (E)? Décrire précisément la figure
d’interférences obtenue.
2. Qu’observe-t-on sur l’écran (E)si l’on obture l’un des deux
trous ?
1

MP1 Lycée Janson de Sailly DM n°13
3. Comment est modifiée la figure d’interférences si on translate la
plaque (P)suivant l’axe Ox ? Suivant l’axe Oy ?
4. Comment est modifiée la figure d’interférences si on translate
l’écran (E)suivant l’axe z0z?
3 Différence de chemin optique
Soit un point Mde l’écran (E), de coordonnées (x, y, 0) dans le
repère (O, ~ex, ~ey, ~ez).
1. Exprimer les distances S1Met S2M, respectivement entre les
trous S1et S2et le point M. On exprimera S1Met S2Men
fonction de a,D,xet y.
En déduire l’expression de la différence de chemin optique
δ(M) = S2M−S1Mau point Mentre les rayons issus de S1
et S2.
On exprimera δ(M)en fonction de a,D,xet y.
2. La distance aentre les deux trous étant petite par rapport à la
distance d’observation D, et le point Métant proche du point
O, on peut considérer que a,x,ysont très petits devant D.
En faisant un développement limité au premier ordre de l’ex-
pression de δ(M)obtenue précédemment, en déduire l’expression
simplifiée de δ(M)en fonction de a,Det x.Cette hypothèse sera
conservée dans la suite.
4 Longueur de cohérence
La lumière émise par le Laser est quasi-monochromatique, formée
de trains d’ondes de durée τc, de fréquence ν0correspondant à une
longueur d’onde λ0= 643,8 nm. La largeur spectrale en longueur
d’onde de cette lumière est ∆λ= 0,05 nm.
1. Quelle est la couleur de cette lumière ?
2. Quelle est sa longueur de cohérence Lc?
3. Quelle est la largeur spectrale en fréquence ∆νassociée, ainsi que
la durée τcdes trains d’ondes ?
4. On prend a= 0,6mm, D= 1,2 m. En déduire la valeur maximale
de xqui permet d’observer des interférences sur l’écran.
5 Intensité lumineuse de l’onde résultante
Dans le cas où |δ(M)|  Lc, on peut modéliser les ondes par
des sinusoïdes. On suppose alors que s1(t) = s2(t) = s0cos 2πc
λt!
représente l’expression des ondes respectivement aux points S1et
S2.s0représente l’amplitude de l’onde considérée et creprésente la
célérité de la lumière dans le vide. On néglige l’atténuation de l’onde
entre les trous et le point M.
1. Déterminer l’expression s1M(t)de l’onde issue du trou S1lors-
qu’elle arrive au point M. On exprimera s1M(t)en fonction de
s0,S1M,c,λet t. Déterminer, de même, l’expression s2M(t)de
l’onde issue du trou S2lorsqu’elle arrive au point M. On expri-
mera s2M(t)en fonction de s0,S2M,c,λet t.
2. En déduire l’expression sM(t)de l’onde qui résulte de la superpo-
sition des deux ondes s1M(t)et s2M(t)au point M. On exprimera
sM(t)en fonction de s0,S1M,S1M,c,λet t.
Mettre l’expression de sM(t)sous la forme du produit d’un terme
indépendant du temps (amplitude de l’onde) et d’un terme dé-
pendant du temps.
3. Sachant que l’intensité lumineuse I(M)(appelée aussi éclaire-
ment) qui résulte, au point M, de l’onde sM(t)est proportion-
nelle à la valeur moyenne du carré de sM(t)avec Kconstante de
2

MP1 Lycée Janson de Sailly DM n°13
proportionnalité, exprimer l’intensité lumineuse I(M)au point
Men fonction de s0,K,δet λpuis en fonction de s0,K,a,x,
λet D.
4. Calculer, en détaillant clairement le raisonnement effectué, l’ex-
pression de l’interfrange ide la figure d’interférences. Exprimer
ien fonction de a,λet D.
5. Tracer l’allure du graphe de I(M)en fonction de x.
6 Inclinaison du faisceau laser
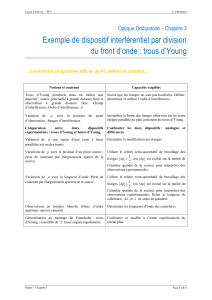
Les rayons du faisceau laser ne sont plus parallèles à l’axe z0z. Ils
sont inclinés d’un angle αpar rapport à cet axe. On se placera dans
le cas où l’angle αest petit.
Figure 2 –
1. Déterminer la nouvelle différence de marche δ(M)en un point
Mde l’écran de coordonnées x,y.
2. Quelle est alors la position de la frange d’ordre p= 0 ?
3. Décrire le plus précisément possible comment est modifiée la fi-
gure d’interférences par rapport à l’étude précédente (rayons pa-
rallèles à z0z).
7 Lumière polychromatique
On revient au montage de la Figure 1 pour lequel les rayons lumi-
neux incidents sont parallèles à l’axe z0z. Ces rayons ne sont plus émis
par un faisceau Laser mais proviennent maintenant d’une source ponc-
tuelle Splacée dans le plan focal objet d’une lentille mince conver-
gente.
Cependant, la source Sn’est plus monochromatique : elle émet des
radiations possédant toutes les fréquences comprises entre ν0−ν1et
ν0+ν1où ν1ν0.
On suppose que, si on obture un des deux trous, l’intensité lumi-
neuse sur l’écran produite par les radiations dont la fréquence est
comprise entre νet ν+ dνest : dI =J0dν, où J0est une constante
indépendante de la fréquence.
1. Justifier le plus précisément possible pourquoi il est possible
d’écrire l’intensité sur l’écran sous la forme :
I(M) = Zν0+ν1
ν0−ν1
2J01 + cos 2πνδ
cdν
2. En déduire que I(M)peut se mettre sous la forme :
I(M) = A1 + V(δ) cos 2πν0δ
c
où Aest une constante à déterminer en fonction de J0et de ν1
et où V(δ)est une fonction appelée facteur de visibilité dont on
donnera l’expression en fonction de la différence de marche δ, de
3

MP1 Lycée Janson de Sailly DM n°13
ν1et de la vitesse de la lumière dans le vide c. On pourra faire
intervenir la fonction sinus cardinal sinc définie par :
sinc(x) = sin(x)
x
On donne : sin(p)−sin(q) = 2 sin p−q
2cos p+q 2
3. Représenter V(δ)en fonction de δ. Pour quelle valeur de δ
obtient-on le premier brouillage de la figure d’interférence ?
4