Exercice 1 : Principe d`une loupe Exercice 2 : Étude de l`œil

1ere S Correction fiche d'exercices : Construction d'images optiques 2008-2009
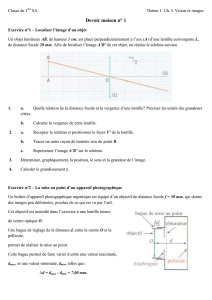
Exercice 1 : Principe d'une loupe
1- Angle Ө sous lequel l'objet est vu :
On a
tan = AB
d=1 25
Ce qui nous donne : Ө = 0,04 rad
2) a) Schéma :
b) L'image A'B' est située à l'infini dans le plan situé en avant de la lentille (cette image est donc
virtuelle).
c) Angle Ө ' sous lequel l'œil voit l'image formée par la lentille :
on a
tan '=OI
OF ' =AB f ' =1 5,0
Soit Ө' = 0,2 rad
d) Comparaison de Ө et Ө ' :
0,2
0,04 =5
soit Ө' = 5 × Ө
La loupe permet donc d'observer l'objet AB sous un angle 5 fois plus grand qu'à l'œil nu et donc d'en
percevoir les détails.
Exercice 2 : Étude de l'œil
1- Schéma :
Le rayon issu de B et passant par le centre optique O n'est pas dévié. Le point B' est donc le point
d'intersection entre ce rayon et la rétine. Le point A' est la verticale de B'.
OF' F
A
BI
Le rayon issu de B qui arrive sur la lentille parallèle à l'axe
optique, émerge de la lentille en passant par le foyer image F'.
La rayon issu de B passant par le centre optique n'est pas dévié.
θ'
A'
B'
F'

2- Position du foyer principal image:
Pour déterminer la position du foyer image, il faut tracer la rayon issus de B et parallèle à l'axe optique.
Sachant que tous les rayons issus de B passent obligatoirement par B', on trace facilement ce rayon, et son
intersection avec l'axe optique nous indique la position du foyer image principal (voir schéma ci-dessus,
rayon en rouge)
3-a) Taille maximale de l'image pour quelle soit vue comme un point :
Une image est vue comme un point si et seulement si elle est détectée par une seule cellule de la rétine.
Une cellule ayant une dimension de 4 μm, l'image formée apparaîtra comme un point si sa taille est
inférieure à 4 μm.
3-b) Taille maximale de l'objet pour que son image soit vue comme un point :
On utilise la relation du grandissement :
= A' B '
AB =OA ' OA
On obtient donc :
AB=A' B '
OA' ×OA
AN :
AB=−4⋅10−6
25⋅10−3×−25⋅10−2
= 4.10-6×101 = 4.10-5 m = 40 μm
3-c) Vergence du cristallin lorsqu'il accommode au maximum :
On utilise la relation de conjugaison
1
OA' −1 OA=1 OF ' =C
AN :
C=1
25⋅10−3−1 −25⋅10−2
C = 44 δ
4- Vergence du cristallin lorsque l'œil n'accommode pas :
On utilise la relation de conjugaison
1
OA' −1 OA=1 OF ' =C
l'objet étant situé à l'infini on a
OA∞
ce qui nous donne
1
OA 0
Et donc
C=1
OA' =1
25⋅10−3
C = 40 δ
Conclusion : Lorsque qu'un objet s'approche de l'œil, celui-ci accommode pour le voir nettement, c'est à
dire qu'il augmente la vergence de son cristallin. Un œil normal a une zone de vision nette qui va d'à peu
près 25 cm (position du punctum proximum) jusqu'à l'infini (punctum rémotum).