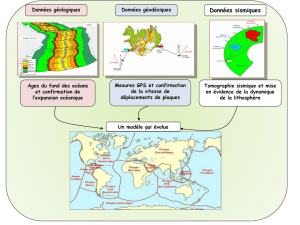
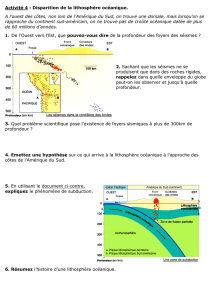
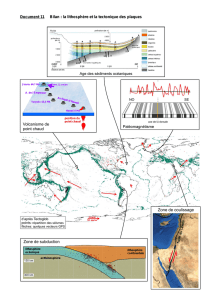
exercice eleve

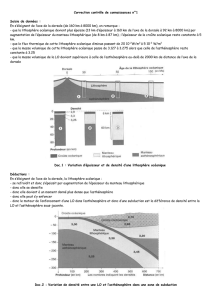
Pourquoi la lithosphère océanique plonge sous la lithosphère chevauchante ?
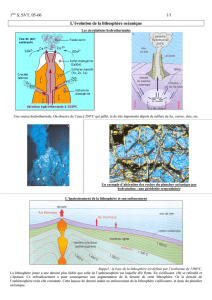
De façon habituelle, un objet chauffé se dilate et un objet refroidi se contracte. Les roches
en s’éloignant de la dorsale se refroidissent par conduction, d’abord très rapidement puis
plus lentement. Ce refroidissement se traduit par un abaissement de l'isotherme 1 300°C qui
représente la limite lithosphère asthénosphère: il s’ensuit un épaississement progressif de la
lithosphère océanique par sa base. proportionnellement à la racine de son âge.
Une colonne de lithosphère, de hauteur H, est constituée d'une croûte océanique d'épaisseur
constante h=5000 m et d'un manteau lithosphérique d'épaisseur (H-h) variable suivant son
âge.
La masse Mlit d'une colonne de lithosphère océanique, de surface égale à 1 m
2
est donc égale,
en kg, à:
Mlit = mcr x h + mlit x(H - h) avec
Masse volumique de la croûte océanique : mcr = 2,85.10
3
kg/m
3
Masse volumique du manteau lithosphérique: mlit = 3,3.10
3
kg/m
3
Épaisseur de la croûte océanique : h = 5000 m
Épaisseur totale de la lithosphère océanique : H = 9200 (âge)
1/2
(valeur expérimentale
modélisant l'épaississement au cours du vieillissement)
Remarque : Les épaisseurs sont exprimées en mètres et l'âge en millions d’années.
La masse Mast de la colonne d'asthénosphère sous-jacente, ayant la même surface et la même
hauteur H que la colonne lithosphérique, est égale à
Mast = mast x H avec:
Masse volumique de l'asthénosphère : mast = 3,25.103 kg/m3.
Compléter le tableau ci-dessous puis répondre à la question titre.
Age de la
lithosphère
En Ma
H= 9200 (âge)
1/2
Mlit x (H-h)
Mlit = mcr x h + mlit x(H - h)
Mast mast x H
10
20
30
40
50
60