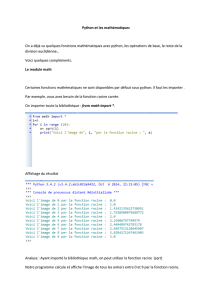
Commencer par créer un répertoire python_1617 dans votre dossier

2017
PC* Travaux dirigés python 1 Mardi 20 septembre
Commencer par créer un répertoire python_1617 dans votre dossier personnel, puis créer un
sous-répertoire «TDx» où xreprésente le numéro du TD, sous-répertoire dans lequel vous
pourrez sauvegarder vos chiers Python relatifs à ce TDx.
Sortir un stylo, du brouillon et de quoi prendre des notes (à conserver !) sur ce que vous
apprenez au fur et à mesure.
Exo 1 On construit une liste d’entiers choisis aléatoirement dans J0,20J:
import random
a = []
for iin range(100):
a.append(random.randrange(20))
On souhaite eectuer un tri des éléments de a, en sachant qu’il s’agit d’entiers positifs.
(1) Déterminer la valeur maximale kdes éléments de a. Construire la liste bde longueur k+1, dans
laquelle chaque case bicontient le nombre d’occurences de idans a.
(2) Déduire de bune liste ccontenant les éléments de a, triée par ordre croissant.
(3) Évaluer la complexité en temps et en espace de cette méthode de tri.
Exo 2 On dénit la suite (fn)n∈Npar :
(f0=f1= 1
∀n∈N, fn+2 =fn+1 +fn.
(1) Écrire une fonction récursive fibo(n) qui calcule fn.
(2) Chronométrer le temps d’exécution de cette fonction pour le calcul de f35.
(3) On note T(n)le nombre d’additions eectuées lors de l’évaluation de fibo(n). Donner la relation
de récurrence satisfaite par T(n), puis l’expression de T(n)en fonction de n.
(4) Reprendre les questions précédentes avec une fonction itérative, et conclure.
(5) Peut-on proposer une fonction récursive qui permette de calculer fnen temps linéaire ?
Exo 3 Considérons l’entier N= 42.
0n a N= 32 + 8 + 2 = 1 ×25+ 0 ×24+ 1 ×23+ 0 ×22+ 1 ×21+ 0 ×20. L’écriture en base 2de
l’entier Nest donc :
101010
On a N= 40 + 2 = 4 ×101+ 2 ×100. L’écriture en base 10 de Nest donc :
42
(1) Écrire une fonction base2(n), qui prend en argument un entier n, et qui renvoie son écriture en
base 2. Expliquer les choix faits concernant les structures de données utilisées. Tester sa fonction
avec N.
(2) Écrire sur le modèle de la fonction précédente une fonction base, qui prend en argument un
entier net un second argument, optionnel, correspondant à la base bdans laquelle on souhaite
obtenir l’écriture de n. Par défaut, il s’agira de l’écriture binaire. Tester sa fonction avec N.
(3) Écrire une fonction réciproque à la fonction précédente. Discuter de l’ecacité de cette dernière
fonction. Tester sa fonction avec N.
2016-2017 1/4

2017
PC* Travaux dirigés python 1 Mardi 20 septembre
Exo 4
(1) Dénir une fonction cherche_mot(w,s) qui teste la présence du mot wdans la chaîne s.
(2) Évaluer la complexité temporelle de la fonction précédente en dénombrant les comparaisons de
caractères.
Exo 5
(1) Dénir une fonction récursive retourne(s), dont l’argument est une chaîne de caractères, et qui
renvoie la chaîne écrite à l’envers.
Ainsi, retourne("python") renvoie la chaîne "nohtyp".
(2) Dénir une fonction est_palindrome(s) récursive, ou faisant appel à une fonction récursive,
dont l’argument est une chaîne de caractères, et qui renvoie le booléen indiquant si sest un
palindrome ou non.
On rappelle qu’un palindrome est un mot qui peut se lire aussi bien de la gauche vers la droite
que de la droite vers la gauche, comme « kayak » ou « radar ».
(3) Discuter de l’ecacité de la fonction proposée.
2/4 2016-2017

2017
PC* Travaux dirigés python 1 Mardi 20 septembre
Rappels de syntaxe / Indications
Exercice 1
•Python est un langage modulaire : de nombreuses fonctions supplémentaires sont dénies dans des
modules que l’on doit importer en début de session intéractive pour y avoir accès (commande import
random par exemple).
Par exemple, le module math contient un grand nombre de fonctions (pour les lister, après import
math, écrire la commande dir(math)) : pour avoir de l’aide sur le module math, taper help(math) et
pour avoir de l’aide sur la fonction sqrt du module math, taper help(math.sqrt).
Pour accéder à la fonction sqrt de math, taper math.sqrt
Dans l’exercice 1, on a importé tout le module random, et on a appelé la fonction random de ce module
à l’aide de random.random
On aurait pu aussi importer tout le module random via «from random import ∗», puis accéder à la fonction random via «random», mais méthode à
éviter (conit potentiel de noms entre plusieurs modules).
•range(30) désigne l’ensemble d’entiers J0,29Kou encore J0,30J.
•Noter également : l’initialisation à la liste vide, la syntaxe de la boucle for (avec le :) et l’indentation !
•python dispose d’une fonction max
•Ne pas oublier l’initialisation de b.
•Pour créer la liste [0,0,0], on peut soit [0] * 3
soit [0 for i in range(3)]
•Avec une liste L, on peut parcourir les indices de cette liste (via «for k in range(len(L))») ou par-
courir les éléments de cette liste (via «for elt in L»).
•Aectations augmentées de variables : s+=1 désigne s=s+1, p*=2 désigne p=p*2 (fonctionne
aussi avec /=, //=, %=,**=, )
Exercice 2
•Pour calculer le temps d’exécution d’une instruction, on peut procéder ainsi :
on import le module time
puis, avant le début de l’instruction (resp. à la suite de l’instruction), on met «debut = time.clock()»
(resp «n = time.clock()»)
puis on ache le résultat via «print(n - debut)»
•Pour une fonction récursive linéaire, on pourra dénir une fonction aux
Exercice 3
1. Si Lest une liste, L.append(a)permet d’ajouter en dernière position l’élément aà la liste L.
L.reverse() permet de «renverser» la liste L.
n%2(resp. n//2) renvoie le reste (resp. le quotient) de la division euclidienne de npar 2.
3 Si L= [ak, . . . , a0]est la liste correspondant à l’écriture en base 2 de n, alors n=
k
X
i=0
ai2i.
2016-2017 3/4

2017
PC* Travaux dirigés python 1 Mardi 20 septembre
Exercice 5
Dans un premier temps, vous pourrez écrire une fonction est_palindrome en O(n2), puis l’améliorer
en une fonction linéaire.
4/4 2016-2017