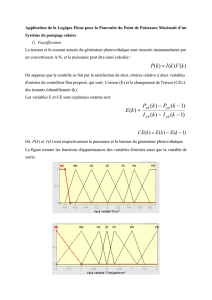
Téléchargement

ELE3204 Automation industrielle Examen final Hiver 2002
ELE4202 Commande processus industriel
Page 1 de 4
Question no 1 (5 points)
La figure ci-dessous représente un chariot se déplaçant sur un rail selon un montage
semblable à celui utilisé au laboratoire.
Figure no. 1
Le moteur à courant continu situé sur le coté droit assure le déplacement du chariot par
l’intermédiaire d’un câble et d’une poulie (rayon = 2cm). Le moteur est muni d’un réducteur 4 :1.
Un encodeur optique (500 imp/tour) est fixé directement sur l’arbre du moteur.
Du coté gauche, un résolveur est relié à une seconde poulie (rayon = 2cm) par un engrenage
réducteur (rapport n :1). Le résolveur est relié à un circuit électronique comprenant un encodeur 14
bits.
i) Déterminer la résolution en mètre de la mesure de position du chariot provenant de
l’encodeur optique en supposant qu’une carte d’acquisition de type QUAD0-04 est utilisée
(résolution maximum).
ii) Déterminer le rapport d’engrenage (n :1, avec n un nombre entier) pour que le résolveur
donne une mesure absolue de la position du chariot sur une plage de déplacement de 6 mètres
(max
x6 mètres
=
). Donner la résolution de cette mesure.
Quel capteur donne la meilleure résolution?
iii) Supposons que le moteur tourne à 1000 tours/minute et pour une période d’échantillonnage
de T=30msec, évaluer la résolution de la mesure de vitesse du chariot (en mm/sec) obtenue
à partir de l’encodeur optique. Donner cette résolution en nombre de bits par rapport à la
vitesse du moteur.
engrenage réducteur
4 :1
résolveur
engrenage réducteur (n
:1)
encodeur
optique
moteur
max
x6m
=

ELE3204 Automation industrielle Examen final Hiver 2002
ELE4202 Commande processus industriel
Page 2 de 4
1
K
s
2
K
s+a
+
Question no 2 (7 points)
Considérer le système de représenter à la figure ci-dessous. Pour identifier les paramètres de ce
système, on désire appliquer une entrée u(k) de type séquence binaire pseudo-aléatoire et mesurer
la sortie y(k). Notez qu’un bruit additif v(t) est présent au niveau de la sortie du système.
Figure no. 2
i) Le système peut être représenté par le modèle entrée-sortie suivant :
1010
-aT
0
-aT
1
-aT-aT
012
-aT
112
y(k) = a y(k-1) + a y(k-2) + b u(k-1)
+ b u(k-2)
avec a = e
a = -(1+e)
b = -K T e(Ka)(1e)
b = K T +(Ka)(1e)
−−
−
Décrire en détail une procédure permettant d’obtenir le modèle entrée-sortie ci-dessus à
partir du diagramme fonctionnel de la figure no. 2. Si possible, faire les calculs pour obtenir ce
modèle.
ii) Pour identifier le système, on désire appliquer la méthode des moindres carrés sous forme
récursive. Décrivez de façon détaillée cette méthode: identifier les dimensions des différents
vecteurs et des matrices, indiquer clairement la séquence des calculs et montrer comment
initialiser l’algorithme. Utiliser les valeurs numériques montrées sur la figure no.3 pour
initialiser l’algorithme.
iii) Sous quelles conditions les paramètres obtenus par la méthode des moindres carrés seront-
ils non-biaisés. Discuter l’influence du bruit de mesure v(t) sur la précision des paramètres
obtenus.
Bloqueur d’ordre zéro
u(k)
u(t)
1
x(t)
2
x(t)
v(t)
y(t)
y(k)
T
+
+
+
échantillonneur

ELE3204 Automation industrielle Examen final Hiver 2002
ELE4202 Commande processus industriel
Page 3 de 4
Figure no. 3
Question no 3 (8 points)
Considérer le système montré à la figure 4a) et représentant un véhicule à deux roues motrices qui
doit suivre un chemin composé de lignes droites. Le modèle linéarisé du système est représenté par
le diagramme fonctionnel de la figure 4b).
a) b)
Figure no. 4
chemin
x
y
K
s+1
τ
1
s
4
s
u(t)
2
x(t)
3
x(t)
1
y(t) = x(t)

ELE3204 Automation industrielle Examen final Hiver 2002
ELE4202 Commande processus industriel
Page 4 de 4
On désire concevoir pour ce système un contrôleur par retour d’état comprenant un
régulateur et un observateur d’état.
i) Écrire le modèle d’état de ce système. Le système est-il commandable et observable.
Justifier votre réponse.
ii) Donner l’expression de la loi de commande optimale qui minimise le critère suivant
-
TT
1
0
J = y(t) Q y(t) + u(t) R u(t) dt
∞
∫
Donner la signification du critère et la fonction des termes Q1 et R. Cette commande est-
elle stable?
iii) Supposons que la sortie suivante est utilisée au niveau du critère J soit
12
y(t) = x(t) + 0.25 x(t)
. Pour cette sortie y(t) et sachant que
0.5
τ
=
, on pose Q1=1 et on fait
varier R de 0 à l’infini (
∞
). Expliquer comment vont varier les pôles du système en boucle
fermée en fonction de R. Esquisser un graphique montrant la variation des pôles en fonction de
R enjustifiant votre construction. Comment pouvez-vous utiliser ce graphique pour choisir les
gains d’un contrôleur par retour d’état?
iv) Pour implanter ce contrôleur par retour d’état, on désire utiliser un observateur d’état
permettant de reconstruire les états du système à partir de la mesure de la sortie. Donner les
équations détaillées de cet observateur. Le vecteur de gain Ke de cet observateur doit être ajusté
selon une configuration de Butterworth. Un bruit de mesure est présent au niveau de la sortie du
système, indiquer comment les pôles seront choisis selon l’intensité du bruit présent sur le
système (bruit faible et bruit plus important). Expliquer une procédure permettant d’obtenir le
vecteur de gain Ke.
v) On désire simuler le système régulateur-observateur. Donner les équations permettant de
simuler ce système avec Matlab. Indiquer de façon précise comment réaliser cette simulation.
vi) Pour le même système, on voudrait tester un contrôleur à logique floue. Dans ce cas l’état
1
x(t)
représente l’erreur latérale entre le véhicule et le chemin à suivre et 2
x(t)
est
proportionnel à la dérivée de l’erreur latérale:
a) Définir en vos propres termes les notions de variables floues et de fonction
d’appartenance. Illustrer ces notions sur le système proposé.
b) Donner un exemple de règle floue. Expliquer en quelques lignes la différence entre un
contrôleur à logique binaire et un contrôleur à logique floue.