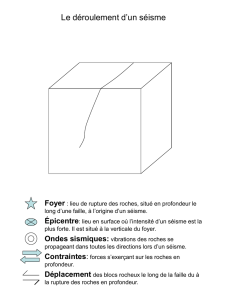
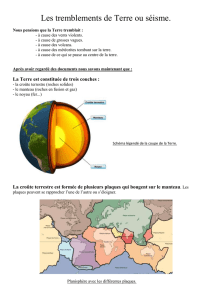
tectonique des plaques

Deuxième partie
LA STRUCTURE DU GLOBE ET SON EXPLORATION
1-La pesanteur et la forme de la Terre (gravimétrie et géodésie)
1.1-La forme de la Terre
1.1.1-Introduction : La Terre selon les anciens, Erasthostène
Les grecs (ou au moins certains d’entre eux) savaient déjà que la Terre est sphérique (cf. le TD
''Mesurer la Terre''). Erasthostène, un grec qui vivait à Alexandrie en Egypte au 2ème siècle
avant J.C. a même obtenu une bonne évaluation du rayon terrestre. L'expédition de Magellan
montre que l'on peut faire le tour de la Terre. Enfin vers la fin des années 50 et le début des
années 60 pour la première fois des avions volent assez haut pour voir la courbure de la Terre.
Erathostene Newton Cavendish
1.1.2-L’ellipsoïde:
Au XVIIème siècle, Newton énonce la théorie de l’attraction universelle. Il note que la Terre
devrait être aplatie à ses pôles, en raison de la force centrifuge qui s’oppose partiellement, au
niveau de l’équateur, à la pesanteur terrestre. Pour que la Terre soit aplatie, il faut bien
évidemment qu’elle puisse se déformer sous l’effet de ces forces, c’est à dire qu’il faut supposer
qu’elle a se comporte, ou au moins qu’elle s’est comportée comme un liquide dans le passé (c’est la
2ème hypothèse qui semble la plus raisonnable pour Newton, qui n’imagine pas que la Terre solide
se comporte en partie comme un liquide). Newton calcule l’aplatissement de la Terre, en
supposant qu’elle est homogène et qu’elle a été parfaitement liquide, et il obtient la valeur de
1/230.
Une polémique s’engage entre les tenants de la théorie de Newton, et les géographes français
(famille Cassini). Ceux-ci utilisent, à la fin du XVIIème siècle, la méthode de la triangulation pour
obtenir des cartes du royaume de France, bien plus précises que celles obtenues jusque là, en
utlisant des la technique du cercle répétiteur, qui permet de faire une mesure avec une précision
de 1'' d'arc. La distance nord-sud de la France, entre Dunkerque et Perpignan, est calculée à
l’aide d’un réseau de triangulation établi en suivant le méridien de Paris (mesure de la Méridienne

de France). Les géographes ont l’impression, à l’aide de ces mesures, que la Terre est allongée
suivant son axe de rotation. Ils remarquent toutefois que leurs mesures sont trop peu précises
pour affirmer cet allongement de manière certaine.
Pour trancher cette querelle, l’Académie royale des Sciences de Paris et Louis XV décident
d’envoyer 2 expéditions scientifiques, l’une près du pôle en Laponie, l’autre en Equateur, pour
mesurer par triangulation la longueur d’un degré d’arc. Alexis Clairaut fait partie de l’expédition
de Laponie, qui revient rapidement, après quelques mois. L’hypothèse de Newton est confirmée,
et Clairaut reprend les calculs de Newton, qu’il affine. L’expédition d’Equateur comprend des
savants célèbres (Bouguer, La Condamine), mais ils n’achèveront leurs mesures qu’après plus de 10
ans de travail.
Intruments de mesure des angles pour la
triangulation
Pierre Bouguer
Au cours du XIXème siècle, les géographes essaient de déterminer les paramètres de l’ellipsoïde
terrestre (longueur A du grand axe, B du petit axe, et valeur (A-B)/A de l’aplatissement.
Les valeurs obtenues sont approximativement : A=6378km ; B=6356km ; aplatissement~1/300.
La forme de la Terre peut être décrite comme un ellipsoïde de révolution.
1.2-La pesanteur
1.2.1-La valeur théorique de g
Le champ de pesanteur à la surface de la Terre est essentiellement dû à la masse terrestre. On
peut calculer, de manière théorique, le champ de pesanteur à la surface de la Terre. Pour cela on
applique la loi de Newton :
2
Mm
F G R =
M est la masse de la Terre, m la masse d'un objet, R le rayon terrestre, et G la constante
d’attraction universelle.
Pour faire ce calcul il faut connaître la masse de la terre et la constante de gravitation
universelle. C'est Cavendish qui a fait cette mesure en 1798. Il a d'abord mesuré la constante de
gravitation universelle en mesurant la force qui s'exerce entre deux masses de métal, puis en a

déduit la masse de la Terre. Comme on connaît la taille de la Terre, on peut calculer la densité de
la Terre. La densité de la Terre globale est de 5.5 soit nettement plus que la densité des plus
denses roches terrestres communes (3.3). On en déduit qu'il existe en profondeur des masses
lourdes. Il s'agit là de l'exemple d'un calcul géophysique.
La valeur de G est de 6.67 10-12 SI (m3kg-2s-2) et la masse de la terre 6 1024 kg. Le poids d'un
objet peut s'écrire P=mg ou g regroupe la masse de la Terre, son rayon et G. On obtient g=9.81
m/s2, ou plutot 981 gal qui est l'unité utilisé pour les mesures de gravimétrie. Comme la terre
n'est pas une sphère, en fait, g=987 aux pôles et g=978 à l'équateur.
1.2.2-Le géoïde.
On peut faire un modèle idéal, en considérant que la Terre à la forme d'un ellipsoïde (ce qui est
vrai) et que toute sa masse est concentrée au centre de la terre (ce qui est faux). On peut ainsi
calculer une gravité théorique en tout points du globe terrestre, à l'altitude 0 (niveaux moyen
des océans). La surface d'isogravité ainsi calculée a la forme d'un ellipsoïde.
g=978031.85 (1+0.005302357sin2λ-0.000005865sin22λ) ou λ est la latitude
Mais on peut aussi mesurer directement la gravité en tout points du globe (actuellement on fait
ceci par satellite), et construire la surface réelle d'isogravité au niveau de la mer. On appelle
cette surface le géoïde On constate que le géoïde est presque un ellipsoïde, mais pas
exactement. Ces écarts sont dues au fait que la terre n’est pas parfaitement homogène, mais
qu’elle renferme des roches de densités variables. Au pied d’une chaîne de montagnes, par
exemple, la masse de roche située au dessus de la plaine dévie le champ de pesanteur en
direction de la montagne. Le géoïde, perpendiculaire à g, est donc en général légèrement plus
haut au dessus d’une montagne qu’au dessus d’une plaine. Toutefois, la déviation de la verticale
est minime, et le géoïde ne se relève en général que de quelques mètres au niveau d’une montagne
(ex. ~+7 mètres dans les Alpes, cf. Figure B8, ~+40 mètres dans les Andes).
Le fait que le géoïde corresponde presque parfaitement à l’ellipsoïde monte que la Terre se
déforme sous l’effet des forces de pesanteur. Elle semble donc se comporter comme un fluide,
ce qui peut paraître étonnant.
Représentation en carte des écarts du Géoïde par rapport à l'éllipsoïde

Représentation des écarts du Géoïde par rapport à l'éllipsoïde
1.2.3-Anomalies de Bouguer
Les écarts entre la valeur théorique et la valeur mesurée de la gravité sont un moyen d'explorer
la répartition des masses en profondeur. Cette technique repose sur le calcul des anomalies de
Bouguer (du nom de Pierre Bouguer, 1698-11758, géophysicien français). Le principe du calcul est
de calculer la gravité en un point en tenant compte de toutes corrections possibles. L'écart
restant nous renseigne sur la répartition des masses en profondeur.
On calcule d'abord la gravité suivant le modèle de l'ellipsoïde, puis on fait les corrections
suivantes:
-on corrige de la force centrifuge, qui a une composante verticale (ω2rcos2λ, ou r est le rayon
local de la terre, ω est la vitesse de rotation angulaire, et θ la latitude. A toulouse la
correction vaut environ 1.8 gal)
-On corrige de l'attraction lunaire et solaire (qui peut atteinde 0.3 mgal)
-On fait la correction d'altitude ou d'air libre ou de Faye, pour tenir compte du fait que l'on
est pas à l'altitude 0 pour laquelle l'ellipsoïde est calculé. C (mgal) = 0.3086h avec h altitude
en m.
-On fait ensuite la correction de plateau ou de Bouguer qui consiste à pendre en compte
l'attraction des terrain situés entre le lieu de mesure et l'altitude 0. Il faut pour cela faire
une hypothèse sur la nature des terrains entre le lieu de mesure et l'altitude 0.
Cb (mgal) = 0.04192 ρ h avec r densité des terrains en kg/m3 et h leur épaisseur.
-Enfin on fait une correction de relief pour tenir compte des montagnes et des vallées.

La différence Gmesuré-Gcalculé est l'anomalie de Bouguer. Si l'anomalie est négative cela veut dire
que la valeur réelle est inférieure à la valeur calculée et donc qu'il y a en profondeur des masses
légères (et vice-versa).
Les anomalies de Bouguer peuvent atteindre des valeurs de l’ordre de 0,003 m/s2, qui restent
modérées par rapport à la valeur totale du champ de pesanteur. On constate que les anomalies de
Bouguer sont en général fortement négatives dans les chaînes de montagnes, faibles dans les
plaines, et positives dans les océans. On en déduit qu’il y a sous les montagnes, de grandes
quantités de roches légères, et des masse lourdes sous les océans.
Carte des anomalies de Bouguer de la France. Noter les anomalies positives dans les bassins
océaniques et les anomalies négatives au niveau des montagnes, d'autan plus grandes que
l'altitude des montagnes est élevée
La notion d’isostasie
Le principe de l’isostasie et sa justification théorique
Les mesures de pesanteur et la forme du géoïde suggèrent donc qu’il existe une racine de roches
peu denses à la base des chaînes de montagne, et que ces montagnes semblent flotter à la
surface de la terre un peu comme des glaçons flottent à la surface de l’eau.