énoncé

Spé y 2009-2010 page 1/4 Devoirn°8
Spé y 2009-2010 Devoir n°8
OPTIQUE
Partie I
LUNETTE ASTRONOMIQUE
Une lunette astronomique est schématisée par deux lentilles minces convergentes, l’une no-
tée L1 et appelée objectif, de distance focale f1’ = 50 cm et l’autre, notée L2 et appelée oculaire, de
distance focale f2’ = 2 cm. Le plan focal image de L1 est confondu avec le plan focal objet de L2. Le
centre optique de L1 est noté O1 et celui de L2 est noté O2. Le point focal image de L1 est noté F1’ et
le point focal objet de L2 est noté F2.
La lunette est utilisée dans les conditions de Gauss,
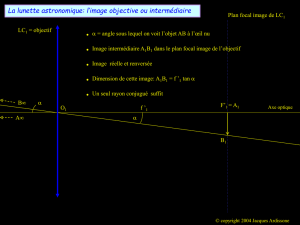
I-1) Sur un schéma qui ne sera pas à l'échelle, représenter le trajet des rayons émergents as-
sociés à un rayon incident parallèle à l’axe optique.
I-2) Sur un schéma qui ne sera pas à l'échelle, représenter le trajet des rayons émergents as-
sociés à un rayon incident qui fait un angle a avec l’axe optique. On notera B1 le point
d’intersection de ce rayon avec le plan focal image de L1 et a’ l’angle que fait le rayon émergent de
L2 avec l’axe optique.
I-3) Déterminer le grossissement (angulaire) G = a’/a en fonction de f1’ et f2’. Calculer la
valeur numérique de G.
I-4) Le rayon des lentilles L1 et L2 sont respectivement R1 et R2 avec R2 = R1/4.
a) Sur un schéma qui ne sera pas à l'échelle, tracer la marche des rayons extrêmes
(c’est-à-dire passant par les bords de L1) de faisceaux issus de sources ponctuelles à l'infini dont la
direction fait un angle a avec l'axe optique de la lunette. Montrer alors que si l’on suppose que tou-
tes les sources ponctuelles émettent avec une même intensité lumineuse, l’éclairement n’est pas
uniforme sur toute la surface de L2.
b) Calculer la valeur a1 de a telle que tous les rayons d’angle a < a1 qui traversent
L1 traversent aussi L2. Quelle condition doit vérifier R2 pour que cet angle existe. Pouvait-on le pré-
voir de manière simple ?
Partie II
MESURE DE LA DISTANCE ANGULAIRE DES COMPOSANTES D’UNE ÉTOILE DOUBLE
On utilise la lunette précé-
dente qu’on dirige vers un groupe
de deux étoiles très voisines S1 et
S2 que l’on suppose ponctuelles.
Elles émettent une même lumière
monochromatique de longueur
d’onde l = 0,6 mm d’intensités
respectives I1 et I2. La face
d’entrée de l’objectif est masquée
par un écran, représenté sur la
figure 1, percé de deux fines fen-
tes de Young, parallèles et perpendiculaires au plan de cette figure 1, qui contient les sources S1, S2
et l’axe optique ; on peut faire varier la distance, notée e, entre ces deux fentes fines notées A1 et A2.
Toute l’étude qui suit se fait dans le plan focal image de L1 de sorte que la présence de l’oculaire n’a
pas d’importance dans cette partie.
Les fentes sont supposées de très grande longueur par rapport à leur largeur.
PLAN FOCAL IMAGE DE L1
M(x)
F1’
e
/2 O1
L1
A
1
A2
figure 1

Spé y 2009-2010 page 2/4 Devoirn°8
On dispose la lunette de sorte que S1 et S2 soient symétriques par rapport à son axe optique.
Celui-ci fait donc les angles e/2 avec la direction de S1 et –e/2 avec celle de S2, e étant la distance
angulaire entre S1 et S2. Le dispositif est représenté sur la figure 1. Seuls trois rayons issus de S1
sont représentés sur cette figure.
II-1-a) Les deux étoiles constituent-elles des sources cohérentes? Que peut-on en déduire en
ce qui concerne les éclairements qu’elles produisent dans le plan focal image de L1 ?
b) On cherche l’aspect du plan focal image de L1 si S1 était seule. Exprimer la diffé-
rence de marche, au point M d’abscisse x, entre les deux ondes issues de S1, passant par A1 et A2, en
fonction de e, e, x et f1’, distance focale de L1. On suppose f1’ >> e et f1’ >> |x|.
c) En déduire l’éclairement au point M en fonction de e, e, x, f1’, l et I1.
d) Déterminer l’interfrange de la figure d’interférences ainsi produite en fonction de
l, f1’ et e. Faire l’application numérique pour e = 6 mm et f1’ = 50 cm.
e) Reprendre les questions II-1-b à II-1-d pour S2 supposée seule.
II-2-a) Déterminer l’éclairement total au point M résultant des deux composantes de l’étoile
double.
b) Observe-t-on des franges d’interférences et si oui, quel est l’interfrange? Justifier
votre réponse.
II-3) On suppose, dans cette question, que les étoiles S1 et S2 émettent un rayonnement de
même intensité.
a) En mettant l’éclairement de la question II-2-a sous forme d’une somme d’un terme
constant et d’un produit de deux fonctions sinusoïdales, déterminer les valeurs maximales et mini-
males de l’éclairement.
b) En déduire le contraste du système de franges et montrer que les franges disparais-
sent pour certaines valeurs de e.
Application numérique : la plus petite distance entre A1 et A2 pour laquelle les franges dispa-
raissent est em = 71 mm. Calculer la distance angulaire entre les deux composantes de l’étoile dou-
ble.
Partie III
POUVOIR SÉPARATEUR DE L’OBJECTIF
On étudie, dans cette partie, quelques aspects de la diffraction à l’infini par l’objectif de la
lunette astronomique et on applique les résultats au pouvoir séparateur de l’objectif.
III-1) Rappeler le principe de diffraction (principe de Huygens Fresnel).
III-2) On considère une onde lumineuse plane, monochromatique de longueur d’onde l se
propageant dans le vide. Cette onde est diffractée par une ouverture plane S située dans le plan
xO1y, O1 étant une origine prise sur l’ouverture diffractante. On observe l’onde diffractée à l’infini
dans la direction du vecteur unitaire
(,,)
u
abg
r
peu incliné sur la normale Oz au plan de la pupille.
Le dispositif est illustrée sur la figure 2.
a) L’onde lumineuse incidente se propage perpendiculairement au plan xO1y. Déter-
miner l’amplitude complexe de l’onde
(,,)
da
abg
diffractée « à l’infini dans la direction »
(,,)
u
abg
r
par un petit élément de surface de l’ouverture diffractante d’aire dS = dx×dy situé au voi-
sinage du point M(x, y) en fonction de a, b, x, y, l, dS et d’une constante S0 qu’on n’explicitera
pas.
b) Que deviendrait l’expression précédente si la direction de propagation de l’onde
incidente définie par son vecteur unitaire
0
u
r
était
(
)
0
000
,,
u
abg
r
avec a0 et b0 non nuls (mais très
petits devant 1) et g0 » 1.

Spé y 2009-2010 page 3/4 Devoirn°8
III-3) L’ouverture diffractante est l’objectif circulaire L1 de la lunette astronomique de rayon
R. L’objectif joue simultanément le rôle de l’objet diffractant et de la lentille qui ramène l’infini
dans le plan focal de la lentille. On observe la figure de diffraction à l’infini dans le plan focal
image de L1. On suppose de nouveau a0 et b0 nuls.
a) Compte tenu de la symétrie du problème, que peut-on dire de la figure de diffrac-
tion dans le plan focal image de L1 ?
b) Déterminer, sous forme d’une intégrale simple en x, qu’on ne cherchera pas à cal-
culer, l’amplitude complexe a’ diffractée à l’infini dans la direction particulière
'(,0,)
u
ab=g
r
en
fonction de a, l, R et de S0’, constante qu’on n’explicitera pas.
c) À une constante multiplicative près, la valeur de a’, réelle, est donnée numérique-
ment dans le tableau ci-dessous avec m = 2p Ra/l:
m00,4 0,8 1,2 1,6 2 2,4 2,8 3,2 3,6 3,83
a’ 1 0,98 0,92 0,83 0,71 0,58 0,43 0,29 0,16 0,05 0
Déterminer l’intervalle dx’ séparant les premiers minima nuls situés de part et d’autre de F1’.
Cet intervalle représente le diamètre du premier anneau noir de la figure de diffraction.
III-4) On applique les résultats précédents au pouvoir de résolution de l’objectif L1. On ob-
serve l’étoile double de la partie II. La face d’entrée de l’objectif n’est plus masquée par l’écran
percé des deux fentes A1 et A2.
a) Déterminer la distance d séparant les images des deux étoiles S1 et S2 dans le plan
focal image de L1, en fonction de e et f1’.
b) Lorsque les étoiles sont d’intensités comparables, les deux images sont supposées
distinctes si le maximum central de la figure de diffraction correspondant à l’une des étoiles coïn-
cide avec le premier minimum nul de la figure de diffraction correspondant à l’autre étoile. Quelle
doit être la valeur minimale de e, notée em pour que les deux étoiles puissent être effectivement sé-
parées.
Application numérique : calculer em et dm pour R = 10 cm, les autres grandeurs étant déjà dé-
finies dans les questions précédentes.
Partie IV
INTERFÉROMÈTRE À DEUX TÉLESCOPES (SYNTHÈSE D’OUVERTURE)
Au lieu d’utiliser une lunette dont l’objectif est masqué par un écran percé de deux fentes,
on couple deux télescopes identiques T1 et T2, de même ouverture circulaire, de diamètre négligea-
u
r
O1
S
z
OBJECTIF DIFFRACTANT
PLAN FOCAL IMAGE DE L1
M(x, y)
x
x
y
y
LENTILLE
O
figure 2

Spé y 2009-2010 page 4/4 Devoirn°8
ble par rapport à la ligne de base a = T1T2 (figure
3). On peut considérer que la lumière est reçue
par un détecteur ponctuel placé au foyer image
de chaque télescope.
La position moyenne de l’étoile double
est repérée par l’angle a, différent de 0, que fait,
avec la normale à T1T2, notée Oz, la direction
OW, O étant le milieu de T1T2. L’écart angulaire
entre les deux étoiles S1 et S2 est toujours noté e.
L’axe Ox est horizontal, orienté vers
l’ouest.; le plan Oxy est parallèle au plan équato-
rial et Oz est parallèle à l’axe des pôles.
On désigne ici aussi par DS la distance OW, xSl la position de S1 selon un axe WxS perpendi-
culaire à la direction OW, et xS2 la position analogue de S2, avec: xS2 = – xS1.
Un dispositif annexe permet de faire interférer les ondes optiques issues des deux foyers
images en introduisant une différence de marche supplémentaire LS fixée.
En outre, le rayonnement est quasi-monochromatique et centré sur la longueur d’onde
l = 0,6 mm. Enfin les étoiles S1 et S2 émettent un rayonnement de même intensité : IS1 = IS2 = IS.
IV-1-a) Expliquer sans calcul pourquoi l’angle a n’est pas constant au cours du temps.
b) Expliquer sans calcul quel est l’avantage optique de rendre les télescopes orienta-
bles (c’est-à-dire que l’axe optique de chacun d’eux fait, à chaque instant, un angle égal à a avec la
verticale du lieu) plutôt que les laisser fixes (les axes optiques restant parallèles à Oz).
IV-2-a) Exprimer, en fonction de l, a, LS, a, e et DS les différences de phase f1 et f2 asso-
ciées à Sl et S2.
b) Montrer que l’éclairement total I s’écrit: 21coscos2 S
S
L
b
II
é+ù
pe
æö
æö
=+p
ç÷
ç÷
êú
ll
èø
èø
ëû
l
, b
et l étant des longueurs que l’on déterminera en fonction de a et de a. Quelle est la variable dont
dépend I ?
IV-3-a) On suppose que a reste très faible. Que devient l’expression de I(a) ? Les télescopes
sont mobiles sur des rails. On recommence la détermination de I(a) pour différentes valeurs de a.
Qu’observe-t-on ? Comment peut-on distinguer une étoile double d’une étoile simple ?
b) Trouver, en milliseconde d’arc, la plus petite distance angulaire que l’on a pu dé-
tecter si la valeur maximale de a est aMAX = 6,10 m. Quel est l’intérêt d’un tel système par rapport à
celui décrit dans la partie II ?
c) On s’arrange généralement pour que LS = –l. Quelle en est la raison ?
x
z
a
S1
S2
W
T
1 T
2
a
figure 3