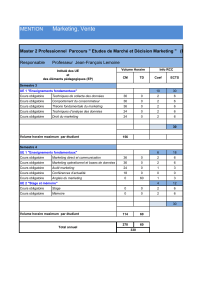
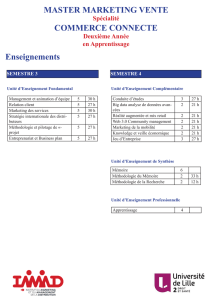
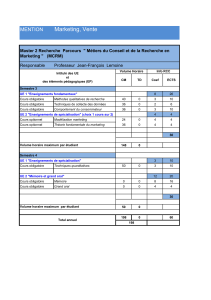
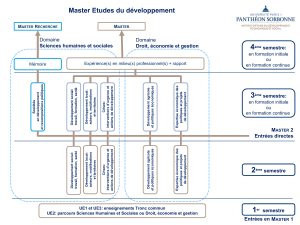
Polycopié avec exercices et examens - Jean

Université des Sciences et Technologies de Lille
U.F.R. de Mathématiques
Deug MIAS 1ère année, 1er et 2ème semestres 2003–2004
Feuilles de TDs, Examens, Corrigés.
Jean-François Burnol
250 exercices, 6 examens, 82 pages. Les feuilles d’exercices comportent aussi des rappels
de cours, souvent très brefs, parfois plus détaillés.

Université des Sciences et Technologies de Lille U.F.R. de Mathématiques
Année 2003-2004 – MIAS (première année)
1er semestre – Section 1
Fiches 1 à 8
Toutes les fiches du premier semestre 2003/2004, 121 exercices. Très brefs rappels de cours.
Jean-François Burnol. Deug MIAS 1ère année 2003-2004. Exercices du 1er semestre. 1

page suivante, S.V.P.
2Jean-François Burnol. Deug MIAS 1ère année 2003-2004. Exercices du 1er semestre.

Université des Sciences et Technologies de Lille U.F.R. de Mathématiques
Année 2003-2004 – MIAS (première année)
1er semestre – Section 1
Fiche 1
Version du 2 oct 2003, 2:26 pm
Deux objets à ces fiches : d’une part récapituler des mots et des notations mathématiques dont la maîtrise
est un objectif pour la bonne compréhension du cours, d’autre part fournir quelques exercices (j’essaie de
ne pas dépasser le format d’une feuille recto-verso, donc les exercices proposés ici ne couvrent pas toutes les
notions). Les théorèmes du cours n’ont pas toujours un nom spécial, leur présence dans les listes de noms
sera ainsi souvent plus implicite qu’explicite. Vous pourrez utiliser ces listes pour jauger au fil du semestre
votre niveau de compréhension : parcourez-les et demandez-vous dans quelle mesure vous en comprenez
les termes (c’est-à-dire leurs interrelations qui s’expriment par des lemmes, propositions, théorèmes).
Lettres grecques (il en manque . . .) : alpha α, bêta β, gamma γ,Γ, delta δ,∆, epsilon ε, êta η,
thêta θ, lambda λ, mu µ, nu ν, pi π,Π, rho ρ, sigma σ,Σ, tau τ, phi φ, psi ψ, oméga ω,Ω.
Proposition (assertion) logique, valeur de vérité, contraire (négation, non-P), et, ou, implication,
contraposée, équivalence, tautologie, P⇒Q,¬P,P⇐Q,P⇐⇒ Q, si Palors Q,Pest
équivalent à Q, tables de vérité, etc . . . axiomes, démonstrations, raisonnements : au cas par cas,
par (réduction à) l’absurde, condition nécessaire, suffisante, nécessaire et suffisante, élégance dans
la rédaction mathématique, mais ou et donc or ni car, cqfd.
Ensembles, éléments, sous-ensembles, parties, singletons, P(E), définition d’un sous-ensemble par
énumération, par propriété, l’ensemble vide ∅, quel que soit ∀, il existe ∃, négations, inclusion
A⊂B, appartenance x∈B, égalité, union A∪B, intersection A∩B, complémentaire ∁A, différence
A\B, lois de de Morgan, partitions, produit cartésien E×F, application, fonction (application
à valeurs numériques), restriction à un sous-ensemble, graphe, injectif, surjectif, bijectif, image,
antécédents, composition, bijection réciproque, fonction indicatrice d’une partie.
L’ensemble Ndes entiers naturels, successeur, prédécesseur, l’ensemble Zdes entiers relatifs. Addi-
tion et multiplication : associativité, commutativité, distributivité, puissances, factorielles. Équipo-
tence, ensembles finis, cardinal, #A(CardA), ensembles dénombrables, coefficients combinatoires
N
k. Indexation de produits Qi∈I, de sommes Pj∈J, expansion de produits en sommes, identités
remarquables, coefficients combinatoires N
k, formule du binôme.
1. On suppose que Pet Qsont vraies. En fonction de la valeur de vérité de Rdéterminer la valeur
de vérité de Ssuivant les cas :
1. S=Pet R
2. S=Qou R
3. S=P⇒R
4. S= (¬Q)⇒R
5. S=R⇒P
6. S= non ((Pou R)⇒(Qet R))
2. Déterminer les négations des assertions suivantes :
1. Si Palors Q
2. Pou non-Q
3. Si (Pou Q) alors R
4. Pimplique Q, et Qimplique R, et Rimplique S.
Jean-François Burnol. Deug MIAS 1ère année 2003-2004. Exercices du 1er semestre. 3