Transistor MOS (cours: Composants - Transistors)

1
1ES102
TRANSISTOR MOS :
MODÉLISATION PHYSIQUE
ET EXPLOITATION NUMERIQUE
ES102 / CM3
Durée ≈ 1h15
2ES102
CONDUCTIVITE DES MATERIAUX
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 2 4 6
10
10
10
10
10
10
10
10
10
10
1
10
10
10
Quartz
Arséniure de Gallium (AsGa)
Silicium (Si)
Germanium (Ge)
Diamant
Silice (SiO2
)
Aluminium (Al)
Cuivre (Cu)
Argent (Ag)
Isolant
Semiconducteur
Conducteur
conductivité σ en Ω-1·m-1
= (résistivité)-1

2
3ES102 CRISTAL DE SILICIUM
• Réseau tétraédrique, où chaque atome met en commun les 4 électrons
de sa couche externe avec 4 voisins
• génération thermique d’électrons libres et de trous (paires électron-trou),
compensée par des recombinaisons
• si champ électrique E, mouvement des électrons libres ET des trous
Si
+4
Si
électron
libre trou
µn ≈ 2µp
trous 2 fois
plus lents que
les électrons pndensité
pe·vp ne·vn courant
vp=µpEvn=µnE
vitesse
µp µn
mobilité
+4
Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si +4 Si
mais que valent n et p ? ↵
4ES102 NIVEAUX D’ENERGIE DANS Si :
STRUCTURE DE BANDES
distance
inter-
atomique
E
dernier niveau
occupé à T=0
premier niveau
inoccupé à T=0
atome Si isolé
cristal Si = 0,543nm
bande de
conduction
bande de
valence
bande interdite
(gap) Eg=1,12eV
semiconducteur conducteur isolant
rapprochement des atomes de Si ⇒
différentiation des niveaux d’énergie,
à nombre total constant (ici 2/atome)
Ec
Ev
5·1010
atomes/µm3
électrons
libres

3
5ES102
DISTRIBUTION DE FERMI-DIRAC
• à T=300K, kT ≈ 25meV d’où Eg=1,12eV≈45kT.
Des électrons peuvent-ils « franchir » 45 kT ?
• La probabilité qu’un niveau d’énergie E soit occupé par un
électron est F(E), où EF , le « niveau de Fermi », est une
constante de normalisation t.q. ∑probabilités = 1 :
• Pour E < EF, ε(E) est la probabilité de présence d’un trou
• n et p : densités d’électrons libres et de trous dans Si
→ n ∝ ε(Ec) et p ∝ ε(Ev), donc n·p ∝ e-Eg/kT qui est
indépendant de EF ⇒ en pratique, n·p constant !
1
1 + e(E-EF)/kT
F(E) = soit ε(E)=e-|E-EF|/kT petit
≈ ε(E) pour E > EF
≈ 1-ε(E) pour E < EF
6ES102
DISTRIBUTION DE
FERMI-DIRAC (2)
-0.1
0
0.1
0 0.5 1
ε(22,5kT) ≈ 1,7· 10-10
Donc seulement quelques électrons
libres par µm3 ⇒ Si est plutôt un isolant
Puisque np est constant, on va rendre n
différent de p pour augmenter µnn+µpp
et en faire un conducteur à volonté :
→ approche statique : dopage
→ approche dynamique : capacité MOS
E-EF
F(E)
Eg
Ec
Ev
T=500K
T=0K

4
7ES102
DOPAGE
+3
B
+5
As
électron libre
en surnombre trou en surnombre
logn
logp
logn
logp
dopage n
dopage p
Si intrinsèque
« Si dopé n »
« diffusion n »
« Si dopé p »
« diffusion p »
ou comment modifier
µnn+µpp à n·p constant
logn
logp +4
Si +4 Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si +4 Si
+4
Si +4 Si
+4
Si +4 Si +4 Si
As « donneur
d’électron »
B « accepteur
d’électrons »
8ES102 CAPACITE MOS
• ou comment piloter dynamiquement µnn+µpp par une tension …
• MOS = Métal-Oxyde-Semiconducteur
• Inversion de population (trous → électrons)
si VGSub > une tension de seuil appelée Vtn
(l’indice « t » signifie « threshold »)
• Version duale sur substrat n (→Vtp)
Grille
(Métal*)
Isolant
(SiO2)
Substrat p
(Semiconducteur)
* du silicium polycristallin a remplacé
depuis 20 ans le métal de la grille
- +
logn
logp
n >> p
n ≈ p
n << p
G
Sub z
VGSub
Poisson :
d2φ/dz2=-ρ/ε
ρ dépend des
niveaux d’énergie
décalés de e·φ
ρ(z)
charge
vol.
φ(z)
potentiel

5
9ES102 TRANSISTOR MOS de type n (nMOS)
Grille
Substrat
p (Sub)
- +
Source Drain
VDS ≥ 0
- +
VGSub
G
SD
Sub
contact
métallique
• Le « canal n » existe : VGSub > Vtn
• La source peut y déverser des électrons : VGS > ≈Vtn
⇒ en pratique, VS = VSub = tension basse
• Le drain les évacue : VDS > 0
IDS
IDS > 0 si 3
conditions
réunies
∆
Sub
Version duale
sur substrat n :
pMOS (de type p)
10ES102
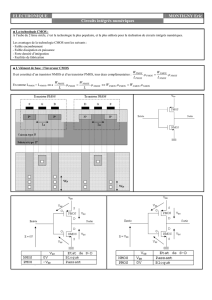
TRANSISTOR MOS NUMERIQUE (1)
•∃! 2 tensions : ‘0’ ↔ GND=0V et ‘1’ ↔ Vdd=1-2V
• Vtn & Vtp ≈ 0,5V ⇒ ±(Vdd-GND) permet de créer un
canal (par inversion de la population initiale de charges mobiles)
• Transistor nMOS passant avec
VSub=VS=GND et VG=Vdd
⇔ connexion à la masse
• Transistor pMOS passant avec
VSub=VS=Vdd et VG= GND
⇔ connexion à l’alimentation
1
0 D ⇔
0
0
1
1
symbole
pMOS
D
D
D ⇔