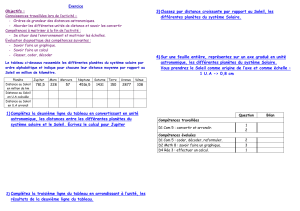
Projet : Eloigner la Terre du Soleil lorsque celui-ci se

Projet : Eloigner la Terre du Soleil lorsque celui-ci se mettra à enfler (dans des milliards
d’années).
Tout d’abord il faut savoir que déplacer un objet tournant autour d’un autre n’est pas simple.
Prenons par exemple deux corps de masse M1 et M2 distant de R et supposons que M2
tourne à la vitesse V autour de M1. Lorsque le mouvement est à l’équilibre, la force
centrifuge (M2*V²/R due au fait que M2 tourne autour de M1) compense la force d’attraction
(G*M1*M2/R²) de M1 sur M2. Donc :
G*M1*M2/R² = M1*V²/R , G étant la constante gravitationnelle
Ce qui est équivalent à V = √(G*M1/R) (*)
Si vous donnez un coup de pied dans M2 en direction de M1, M2 va se rapprocher de M1 et
celle-ci va donc attirer M2 avec plus de force, comme si vous donniez continuellement (et de
plus en plus fort en fait) des coups de pieds dans M2 dans la direction de M1 : Il aura donc
suffit d’un seul coup de pied (d’une force quelconque) et M2 tombe sur M1 très rapidement.
Le raisonnement est le même si vous voulez éloigner M2 de M1 en tapant M2, M1 étant
derrière nous.
En conclusion, pour rapprocher (resp éloigner) M2 de M1 sans qu’il soit happé par (resp
éjecté de l’attraction de) M1, il faut non seulement taper M2 vers M1 (resp dans la direction
opposée) mais aussi augmenter (diminuer) sa vitesse V donnée par (*). C’est ce qui se passe
dans le système solaire : les premières planètes tournent plus vite que les dernières, quelque
soit leur masse (car vous remarquerez que dans (*), la masse M2 n’intervient plus mais
seulement sa vitesse et sa distance à M1).
Il faut maintenant remarquer l’étonnante stabilité du système solaire : par exemple, lorsque
nous nous rapprochons de Venus (entre le Soleil et nous), cette dernière nous attire vers elle,
tel un coup de pied sur la Terre en direction du Soleil. Théoriquement, si l’on suit mon
raisonnement précédent, nous devrions tomber (nous serions déjà tombés, en fait, depuis un
bout de temps) sur le Soleil. Mais c’est sans compter sur Mars ou Jupiter, lointaine mais plus
grosse, qui compense ce « coup de pied » par un autre (pas forcément au même moment), de
l’autre côté de la Terre. Le système solaire (qui inclus les neuf planètes, le vent solaire, les
météorites) doit certainement pouvoir être mis en équation. Une très longue équation dont
les paramètres (masses, distances des planètes) ne pourront jamais être connus exactement.
Cette équation pourrait nous faire croire que le système est stable. Or, pas du tout. Tel une
bille sur une aiguille, ce système est instable et tient miraculeusement la route. Cette stabilité
apparente n’est due qu’au facteur temps sur lequel il a pu compter pour se former (5
milliards d’années): donnez-moi 5 milliards d’années et je vous construis une bille sur une
aiguille, molécules après molécules. Donc ne nous trompons pas : les planètes, les météorites,
la perte de masse du soleil, le vent solaire ou la résonance magnétique des planètes ont
chacun un rôle à jouer dans cet équilibre.
Et inutile de penser que lorsque vous donnez un coup de pied (de force F) à la Terre, celle-ci
va se déplacer : vous même recevez le même coup de pied (de même force mais opposé :-F)
et le système {Terre vous} ne reçoit donc aucun coup : F+(-F) = 0. Encore heureux.
Supposons que le Soleil va voir son rayon augmenté de 100.000.000km et qu’il faille
s’éloigner d’autant (pour que la Terre reste sur sa nouvelle orbite, sa vitesse orbitale aura, au
cours de son déplacement, été préalablement diminuée de 67070m/s.). Que l’affaire doit être

bouclée en 100.000.000 d’années, durée minimale de l’expansion du Soleil. L’effort à fournir
constamment sur la Terre dans la direction opposée à sa vitesse orbitale doit donc être :
6*10^24*6700/100000000/365/24/60/60=10.000.000.000.000N=F. Ou dix fois plus pendant
2h/jour (entre 5 et 7h du matin), en supposant que le jour dure 24h dans des milliards
d’années. N’allez pas croire que F est énorme : 1.000 avions créent un effort d’attraction de
1.000.000.000N sur la Terre. Mais on ne peut pas déplacer la Terre ainsi, l’air puis la Terre
subissant ce même effort, mais opposé, ce qui annule l’effort d’attraction.
Il faut voir que si F est appliquée pendant quelques temps dans la direction Soleil-Terre, la
Terre se place sur une orbite sur laquelle la force centrifuge l’emporte sur la force d’attraction
et prend donc le relais et s’accumule avec le temps. Un éloignement de 100.000.000km est
donc très facile à obtenir (dans une première approximation de 1km/an, vitesse obtenue au
cours, par exemple, d’un millénaire, la poussée désirée nécessite un effort inférieur à F).
L’enjeu majeur est donc de réduire la vitesse orbitale de la Terre. Et de bien doser
l’éloignement et la décélération de la vitesse orbitale car sinon, nous serons tout bonnement
éjectés du système solaire ou happés par le soleil. Mais le risque est à prendre : qu’aurons
nous alors à perdre?
Il y a deux façons de faire:
Rappelons-nous qu’un accélérateur de particules subit le même effort, mais en sens opposé,
que le flux qu’il accélère. Tel le mouvement de recul d’un canon tirant un boulet. C’est ce
recul que nous allons utiliser.
-Soit on expulse de la matière à partir du sol avec des accélérateurs pointant vers le ciel (afin
de dépasser la vitesse de libération mais aussi afin d’économiser de la matière) et en ce cas il
faut construire des tubes à vide (quelques centimètres de diamètre suffisent) qui
chapeauteront nos accélérateurs, avec vue sur l’espace (soit donc une structure ressemblant à
la Dame de Fer d’une hauteur entre 30 et 130km: 30 parce que l’atmosphère est à 99% en
dessous de cette limite, 130 parce que c’est la hauteur à partir de laquelle un satellite peut
raisonnablement faire des ronds. La base devra donc avoir une base de 10 à 50km de large).
Il est impératif d’expulser le flux de la Terre car s’il heurte l’air, qui appartient à la Terre, cela
revient à annuler l’effort exercé par l’accélérateur, comme pour les avions ou le canon tirant
sur une plaque qui lui serait attachée. Pour un accélérateur de 10m, une vitesse de sortie de
200.000km/s (soit donc une vitesse moyenne de 100.000km/s et donc un parcours en
0.0000001sec), l’accélération est de 10^15m/s² . Avec un flux de l’ordre du dixième de
milligramme, l’effort m*acc est donc de 100.000.000N, 10 fois plus puissant qu’un gros
moteur de fusée. En principe, nous pourrions obtenir l’effort que nous voudrions, mais
l’accélérateur risque de s’effondrer sur lui-même. Limitons-nous donc à 100.000T de poussée.
Avec 1.000.000 d’accélérateurs du genre et dont chacun des tubes à vide repose sur la
structure, l’effort total peut donc atteindre les 100.000.000.000.000N, l’effort cherché. Masse
totale éjectée : 20 milliards de tonnes. Mais en superposant les accélérateurs par centaine (ce
qui donne un accélérateur de 1km fonctionnant de manière cadencée sur des tranches de
10m) et en augmentant leur tension de manière à faire approcher la vitesse de la lumière à la
matière accélérée (ce qui lui permet artificiellement d’augmenter sa masse), nous pourrions
diminuer de façon drastique (parions sur un facteur d’au moins 1.000.000 lettres) la masse
des jets, car il faut tenir compte du fait que le « flux » n’est alors plus continu mais discret,
accéléré par jet, ce qui n’empêche pas de le voir comme étant continu car lorsqu’un jet se
trouve dans le dernier tronçon d’un accélérateur, un autre jet peut commencer son départ
pour l’espace dans le premier.
Principaux inconvénients : la composante horizontale de l’effort appliquée sur les tronçons. Il
y a aussi le fait que si on empile les accélérateurs, les matériaux doivent subir un effet

marteau-piqueur, vu que l’effort est tantôt nul tantôt énorme, même si les périodes sont très
courtes. Ensuite il faudra que nous ayons une énergie à la fois importante et non polluante (je
pense à l’énergie à plasma ou à anti-matière, que nous avons des milliards d’années pour
maîtriser). Mais bon, il s’agit d’obstacles techniques. Et l’Homme en a vu d’autres. Et puis on
peut très bien penser que l’homme du futur ne veuille tout simplement pas d’une énergie
trop puissante et se contentera de faire fonctionner avec ses jambes des dynamos
(1.000.000.000 humains générant chacun quelques dizaines de watts...). Mais il faudra aussi
penser, quand viendront les premières éjections, à détruire tous les avions et missiles, à
veiller qu’il n’y a plus d’inégalités qui puissent générer des revendications, bref à s’assurer
qu’il y a la paix totale sur Terre. Parce que sinon, les chances que la (ou les, si nous sommes
prévoyants) tour soit gravement endommagée ne serait-ce qu’une seule fois en 100.000.000
d’années deviendront, connaissant la stupidité de l’homme carnivore, strictement non nulles.
Et je donne alors pour pas cher l’avenir de la Terre.
-Soit on suit le principe donné par ce schéma :
Ici, les particules ne sont pas éjectées du sol mais d’une masse M hors de l’atmosphère qui,
pour se maintenir à une hauteur constante mais ayant une vitesse orbitale nulle autour de la
Terre, doit constamment se propulser dans la direction opposée à l’effort d’attraction de la
Terre. Pour faire bouger cette dernière, il faut que les gaz de propulsion ne la (ou son
atmosphère) heurtent pas et il y a déplacement vers la masse suivant un effort G.M.Mt/R².
Une fois de plus, pour que les gaz quittent facilement le système {Terre, masse}, la masse M
sera dotée d’accélérateurs. Mais même si nous respectons les calculs précédents, notre
satellite doit peser... très lourd. Mais vraiment très lourd. Beaucoup trop, en fait. Par contre,
il faut tenir compte de Jupiter et du fait qu’il est étonnant que le système solaire soit resté
aussi stable pendant des milliards d’années. Il faut croire que la configuration actuelle des
planètes doit pouvoir être régie par une longue équation, de sorte que si nous bougeons la
Terre, tout peut s’écrouler. Donc, puisque Jupiter et les planètes qui la suivent, risquent de
nous tomber sur la tête et que nous ne pouvons pas y construire de réacteurs, je propose
d’utiliser ce deuxième principe : une masse M (quelconque, quelques tonnes) à maintenir
pendant quelques siècles (à la position de l’équivalent de nos 3h, heure locale, afin
d’augmenter la vitesse orbitale de Jupiter et la tirer vers l’infini) et, hop, exit les grosses
boules, qui décrochent de leur orbite.

Avec l’extravagante puissance des ordinateurs du futur (qui modéliseront notre longue
équation moins les grosses boules) et de la durée de l’opération, il n’y a pas lieu de s’apeurer
d’un éventuel décrochage de la Terre.
Restent Mars et la ceinture d’astéroïdes qui sont sur notre chemin de recul. Concernant Mars,
si on ne veut pas l’éjecter, on lui applique le premier principe et il y a des chances que nous
arrivions à la faire graviter autour de nous (à la seule condition que les conditions de vie y
soient les mêmes que sur Terre car sinon les experts qui s’occuperont des propulseurs
oublieront que la Terre est un paradis et feront des erreurs). On peut aussi s’en servir pour
freiner notre éloignement, comme un carreau à la pétanque gravitationnelle. Je rigole. Et les
astéroïdes ? Trop simple : nous les éjecterons un par un, aussi nombreux soient-ils (répétons
le : ON A LE TEMPS ) ou on se constitue une micro planète qui ira aussi graviter autour de
nous. Plus on est de fous...
Petite parenthèse sur les astéroïdes qui menacent la Terre. Si nous arrivions à construire deux
accélérateurs (l’un dirigeant son faisceau en direction d’un astéroïde menaçant et l’autre,
construit diamétralement opposé au premier pour maintenir la position sur l’orbite), sur la
deuxième lune de la Terre (un astéroïde de 5km de diamètre) et d’autres, plus petits (des
accélérateurs en veux-tu en voilà, quoi), pour l’orientation, nous pourrions ne plus en avoir
peur : une force de 100.000.000N pendant 10 jours (suivant, dans le pire des cas, un angle de
1° avec la trajectoire) sur un objet de 10km de diamètre fait dévier ce dernier de 100 mètres,
suffisamment pour changer sa trajectoire mal intentionnée (s’il est encore assez loin).
Maintenant fini l’amusement.
Les satellites artificiels que nous expédions très loin ont besoin de vitesse et, pour cela, se
voient subir des trajectoires compliquées en passant à proximité de planètes afin d’en être
attirée en leur passant derrière, en les contournant avec un dosage attraction/centrifuge et
quittant leur attraction, une fois de plus, derrière elle. Mais il n’y a pas de secret : rien ne se
perd, tout se transforme : si le satellite gagne ainsi en vitesse, la planète « hôte » en perd. Peu,
mais en perd. Pour en revenir au début du texte, la planète reçoit donc un coup de pied. S’il
est bien placé, la planète change d’orbite et y reste (il m’étonnerait beaucoup que nos
scientifiques maîtrisent à ce point la mécanique céleste, pleine de paramètres inconnus). Mais
même en supposant ce meilleur des cas, nous donnons comme une pichenette à ma bille sur
son aiguille. Suffisamment pour la faire tomber ?
Dans le doute, ne devrions-nous pas interrompre les programmes spatiaux interplanétaires?
Parce que si Mars, planète sur laquelle se sont déjà « appuyés » plusieurs satellites venait à
tomber sur le Soleil, elle nous emmènerait avec elle. Quand ?
Je vais vous dire une chose : si nous ne percevons aucun signal d’autres civilisations, peut-
être est-ce parce qu’elles se sont toutes plantées sur ce point et sont toutes tombées sur leur
Soleil. Pas de pitié pour ceux qui font des erreurs. J’entends ça souvent. Pas vous ? Ce n’est
pas moi qui le dit : la Nature est ainsi faite.
Source : clo wan [[email protected]]
Diffuse sur : www.innovationsante.com (2002)