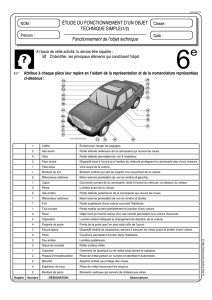
Solides en contact Mouvement « plan-sur

OS, 17 janvier 2006 133
Solides en contact
• Soient deux solides S et S0 restant constamment en contact
– On choisit l’un des deux solides, S0,
comme référentiel
 S0 est immobile et on décrit
le mouvement de S par rapport à S0
– On admet que le contact est ponctuel.
Soit A le point de S en contact avec S0
au temps t.
•v
A = vitesse de glissement (de S par rapport à S0)
• Condition du roulement sans glissement: vA = 0
– A est alors sur l’axe instantané de rotation
• Vecteur instantané de rotation 
– Décomposition en composantes parallèle
et perpendiculaire au plan tangent à S en A:
// = vitesse angulaire de roulement
 = vitesse angulaire de pivotement
S0S
A
référentiel vA
S0S
A
référentiel
//
OS, 17 janvier 2006 134
Mouvement «plan-sur-plan»
•Définition: mouvement tel qu’un plan du solide S reste
constamment dans un plan fixe  du référentiel
à tout instant les vitesses de tous les points du
solide sont parallèles à un plan fixe 
• Conséquences:
– le vecteur instantané de rotation  est perpendiculaire à 
– on est ramené à l’étude du mouvement d’une surface plane rigide 
(section de S) sur un plan ;
– dans ce plan, il y a un centre instantané de rotation (si   0)
• Lieu géométrique des centres instantanés de rotation:
– dans le référentiel lié à : la base
– dans le référentiel lié à : la roulante «Tout mouvement plan-sur-plan
est un roulement sans glissement
de la roulante sur la base»

OS, 17 janvier 2006 135
Exemple: cylindre sur un plan sans glissement
• En trois dimensions:
– Un cylindre S de rayon R roule sans
glisser sur le plan Oxz, avec la
génératrice de contact parallèle à l’axe z
– Il s’agit d’un mouvement plan-sur-plan:
à chaque instant, toutes les vitesses sont
dans le plan Oxy  la base du cylindre
reste constamment parallèle au plan Oxy
–
(pas de pivotement)
• Dans le plan Oxy (plan )
– On considère la section  du cylindre
– Le point de contact C a une vitesse nulle
(pas de glissement); c’est le centre
instantané de rotation
–
r
=  ˆ z = vitesse angulaire de roulement
r
v
P
= r  CP  P  
plan 
centre instantané
de rotation
C
A
B
vA = R
vB = 2R
vC = 0
x
D
zx
y
O
S
R
par ex. r v
D = r
 CD = 0 0  R R
0
= R R
0
Base = axe x
Roulante = circonférence du disque 
OS, 17 janvier 2006 136
Détermination du centre instantané de rotation
pour un solide en mouvement plan-sur-plan dont
on connaît les vitesses de deux points A et B
Au tableau
dA = droite passant par A et
perpendiculaire à vA
Tous les points P de cette droite
ont des vitesses ayant une
projection nulle sur cette droite
(égale à celle de vA)
Idem pour la droite dB
Le point commun à dA et dB a
donc une vitesse nulle. C’est le
centre instantané de rotation It.
A
B
vB
vA
dB
dA
It
P
r
v
P = r
 ItP  vP =  ItP  vP
vA
= ItP
ItA
r
v
P
= r v
A
+ r  AP  r v
P
 AP = r v
A
 AP
Les projections des vitesses de deux
points quelconques du solide sur la
droite qui les relient sont égales

OS, 17 janvier 2006 137
Direction de L
• Deux masses m telles que
par rapport à C
• Axe de rotation  par C faisant
un angle  quelconque avec
•
• On ajoute deux masses m
supplémentaires, de sorte à faire
un système symétrique par
rapport à l’axe de rotation
•
r
r
1
=  r r
2
r
r
1
L =
r
L
C  ˆ
= 2md
2  = I
r
L
C n'est pas parallèle à r
L =
r
L
C  ˆ
= 4md
2  = I
r
L
C est parallèle à r
:
r
L
C = I
r
C
LC,1 LC,3
LC,2 LC,4
mm
mm
LC
r1 r3
r2r4
d
v1
C
LC,1
LC,2
m
m
LC
r2
r1
d
r
L
C,1
= r r
1
 mr v
1
L
C,1
= r
1
mv
1
LC,1
()
z = sin r1
d
1 2 3
mv
1
d
{
= md2 
r
r
2 = r
r
1
r
v
2 = r
v
1
r
L
C,2 =
r
L
C,1
OS, 17 janvier 2006 138
Gyroscope
• Solide «suspendu» à son centre de masseG,
libre d’adopter n’importe quelle orientation,
en rotation autour d’un axe de symétrie (fixe
par rapport au solide) tel que
• Théorème du moment cinétique:
démo
r
L
G
= I r
G
F
Mg
L
d
r
L
G
dt =
r
M
G
ext
= 0 
r
L
G
= constante
• Gyroscope à l’équateur:
– axe de rotation horizontal
selon la direction est-ouest
– 6 heures plus tard,
l’axe est devenu vertical
(à cause du mouvement de la Terre)
Terre
S
N
donc r = constant
e

OS, 17 janvier 2006 139
Effets gyroscopiques (1)
• Roue de vélo en rotation au tour de son axe de symétrie:
– On veut changer la direction de l’axe de rotation; comment faut-il exercer
le couple de force pour que l’axe tourne autour de Ox ? ou de Oz ?
démos: roue de vélo simple
roue de vélo double
r
L
G // r
z
y
x
L
F
F
z
y
x
L
F
F
a) forces F parallèles à z b) forces F parallèles à x
M selon x  dL selon x
 L tourne dans le plan xy
M selon z  dL selon z
 L tourne dans le plan yz
M
dL dL
M
rr
d
r
L
G
dt =
r
M
G
ext = r
r 
r
F
()
+ r r  
r
F
()
= 2 r r 
r
F
Théorème du
moment cinétique
OS, 17 janvier 2006 140
Effets gyroscopiques (2)
• Pourquoi le tabouret tournant (à l’arrêt
quand l’axe de la roue est horizontal)
se met-il en rotation quand on force
l’axe de la roue à être vertical ?
démo: roue de vélo et tabouret
tabouret
à l’arrêt tabouret tourne
– 3ème loi: si la personne applique des
forces sur la roue, la roue applique des
forces égales et opposées sur la personne
(qui la font tourner sur son tabouret)
M = dL
dt = L d dt = L 
r
M = d
r
L
dt =
r
r
L
y
x
z
L
dL
L+dL
d
M
F
F
z
– Conservation de L: si le tabouret peut tourner sans frottements
sur son socle, la composante z du moment cinétique du système
roue+personne+tabouret est conservée (Lz,tot =0)
r
tot
= r +
r
 r
Attention: axe de rotation modifié !

OS, 17 janvier 2006 141
Effets gyroscopiques (3)
• Toupie symétrique avec un point fixe:
– Le moment du poids par rapport au point fixe est constamment
perpendiculaire au moment cinétique (supposé selon l’axe de rotation
propre)  la norme du moment cinétique reste constante: Lc = I
– L’axe de rotation propre a un mouvement de précession autour de l’axe
vertical (de vitesse angulaire )
• Note: on a négligé le moment cinétique
causé par la rotation  !
Résultat approximatif valable si  << 
– Cas général:  n’est pas constant mais oscille
entre deux extrêmes et un mouvement de nutation
se superpose encore
• Toupie sans point d’appui fixe, avec frottement sur le sol
démos: roue sur support réglable
toupie
anagyre
r
M
C = d
r
L
C
dt =
r
r
L
C
CG Mg sin =  LC sin
 = Mg CG
L
C
= Mg CG
I
Lc
G
C = point fixe
Mg
dLc/dt
Mc = CG  Mg ( Lc)
OS, 17 janvier 2006 142
Position d’un solide et angles d’Euler
• Repère lié au référentiel Oe1e2e3
• Repère lié au solide Ay1y2y3
• Repère Ax1x2x3 tel que xi // ei
OP = OA + AP = a
i
(t) ˆ e
i
i
+ y
i
ˆ y
i
i
(t)
• La position d’un point P du solide est
donnée par
c’est-à-dire par les trois coordonnées du
point A dans le repère Oe1e2e3 et par
l’orientation du repère Ay1y2y3 par
rapport au repère Ax1x2x3.
• Cette orientation peut être caractérisée
par les trois angles d’Euler (,,);
on passe de Ax1x2x3 à Ay1y2y3 par les
trois rotations successives suivantes:
plan x1x2
x1
x2
x3
y1
plan y1y2
y2y3
A
u (= axe nodal)
référentiel
e1
e2
e3
O
 [0,2]
 [0, ]
 [0,2]
– Rotation d’angle  autour de l’axe y3
amenant u sur y1
– Rotation d’angle  autour de l’axe x3
amenant x1 sur u (=axe nodal)
– Rotation d’angle  autour de l’axe u
amenant x3 sur y3