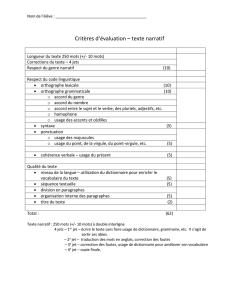
Modèle d`optique-physique de la diffusion au voisinage de l`angle

13
ième
Congrès Francophone de Techniques Laser, CFTL 2012 - ROUEN, 18 – 21 Septembre 2012
Modèle d'optique-physique de la diffusion au voisinage de
l'angle critique de bulles elliptiques
Fabrice ONOFRI
1
, Stefan RADEV
2
, Séverine BARBOSA
1
, Matthias SENTIS
1
IUSTI-UMR 7343, CNRS & Aix-Marseille Université, Technopôle Château Gombert, 13453 Marseille, France
Institute of Mechanics, Bulgarian Academy of Sciences, 4 Acad. G. Bonchev Str., 1113 Sofia, Bulgaria
1 Introduction
La singularité de la diffusion d’une bulle au voisinage de l’angle critique trouve son origine
dans le caractère semi-discontinu [1] des coefficients de réflexion des ondes
=
0
p au voisinage de
l'angle de réflexion totale, soit φ π θ π
−
= − = − ≈ °
1
2 2sin 82
c c
m pour une bulle d’air dans l’eau, d’indice
relatif
= <
/ 1
b s
m m m . Les propriétés de diffusion des bulles sphériques peuvent être modélisées
rigoureusement avec la théorie de Lorenz-Mie (TLM). Bien que moins précis, d'autres modèles ont
été développés pour modéliser ce phénomène, comme l'approximation au premier ordre de la
théorie du moment complexe angulaire [1] ou l'approximation d'optique physique (POA) [2-5]
introduite par Marston [2-3]. Quant à l'optique géométrique [6], elle est par incapable de décrire les
propriétés du champ diffusé au voisinage immédiat de l’angle de diffusion critique où le caractère
ondulatoire de la lumière « s’exprime » fortement (via un effet tunnel notamment [7]). À l’aide de la
TLM et/ou de la POA, les auteurs ont proposé et validé le principe d'une nouvelle technique
optique permettant de reconstruire la distribution de taille et mesurer l'indice de réfraction moyen
d'un nuage de bulles sphériques (technique CARS [4-5, 8-9]) et ceci, de manière quasi
instantanée et avec très peu de ressources informatiques. Cependant, du point de vue théorique
ou applicatif, le modèle de la bulle sphérique s'avère insuffisant dès lors que l'on s'intéresse aux
écoulements gravitaires de grosses bulles (plus de 700-800µm pour des bulles d’air dans de l’eau)
ou fortement cisaillés [9-10].
Pour répondre à cette problématique, nous présentons dans cet article un modèle d'optique
physique permettant de décrire la diffusion, dans le champ lointain et au voisinage de l’angle
critique, de bulles (ou jets) à section elliptique (voir la figure 1) [12].
2 Modèle de diffusion
La figure 1 présente la géométrie du problème étudié. La bulle d’ellipticité γ =
/
x y
a a
et
d'équation dans le plan
(
)
(
)
+ =
2 2
0 0
/ / 1
x y
x a y a , peut être oblate γ
>
1
ou prolate γ
<
1
. Son rayon de
courbure local s’écrit =
3
2
0
0
2
x y
aaN
R avec
(
)
(
)
2 2
2 2 2
0 0 0
/ /
x y
N x a y a
= + pour le module de la normale
correspondante. L'onde incidente est plane et de polarisation quelconque. Les contributions des
rayons d'ordre
>
1
p sont négligées dans cet article, dans le mesure où, nous ne nous intéressons
qu’au phénomène de diffraction scalaire.
La première étape s’attache à décrire la forme du front d'onde de l'onde réfléchie (rayons
=
0
p ) au voisinage du point d'impact
(
)
,
c c
x y
associé à l'angle critique
c
θ
. En s’appuyant sur la
méthode introduite par Airy [11] dans sa théorie de l'arc-en-ciel, et celle de Marston [2] pour des
1
Correspondant : [e-mail]

13
ième
Congrès Francophone de Techniques Laser, CFTL 2012 - ROUEN, 18 – 21 Septembre 2012
bulles sphériques, ce front d'onde est décrit dans un repère orthogonal
(
)
,
u v
. La direction de
v
est
donnée par le rayon critique impactant en
(
)
,
c c
x y
, sachant que
θ θ
= − +cos2 sin2
c f c f
v x y
et
θ θ = +sin2 cos2
c f c f
u x y
[12]. En utilisant un développement en série de Taylor, le front d'onde
(
)
=
v v u
pour →
0
c
u est décrit par :
( ) ( ) ( ) ( )
= + − + − + −
2
2 3
2
1
2!
c c c c
dv d v
v v u u u u u O u u
du du
(1)
S’il est aisé de monter que
(
)
ν
= = =
0
c c c
v u u , il est plus délicat de démontrer que
=
=
/ 0
c
ü u
dv du et
(
)
=
<
2 2
/ 2 0
c
ü u
d v du . Le but ici est bien évidement de déterminer le terme quadratique :
γ
α
==
=
=
0
2
2
20
0
1
1
2
2!
c
uc
x x
dp
d v
dx
q
du
(2)
Où, pour simplifier les notations, nous avons introduit les quantités : =
0
/
q du dx
et =
0
/
p dv dx
, avec
= = −
2
2 3
0 0
1
;
dv p d v dp dq
q p
du q du q dx dx
(3)
En utilisant l’équation canonique de l’ellipse, il vient que [12] :
θ θ
θ θ
=
=
=
=
=
=
= − +
= +
0
00
0
00
0 0
0 0
cos2 sin2
sin2 cos 2
c
c x x
c
c
c x xc
f f
c c
x x
x x
f f
c c
x x
x x
dx dy
pdx dx
dx dy
qdx dx
(4)
avec
=
=
=
=
=
= − +
=
−−−
= − + +
0
0
0
0
2
4 2
0
22
2 2 2 2 2 2
0
2
2424
0
4 2 2 2
2
22 2 2 2
2 3 2 2 4 2 2
2
0¨
2;
1 1 1
8
1 1
2
4
c
c
c
c
cf
x c
x x
y c cf
x c c y x x y
x x
fc
c y x
x x
y y c c
c c
fx y y x
x c x y c x c c
x x
xdx
dx a N
a x xdy
dx a N y a a a a
d x x
dx N a a
a a y x
x y
d y a a a a
a y a a N a N y
dx
(5)
A l’aide des équations (2)-(5), nous pouvons déterminer la valeur du terme quadratique du
développement en série. Plusieurs remarques importantes peuvent être faites à ce niveau :
- Le front d’onde associé à la diffusion critique est quadratique, alors qu’il est cubique
pour l’arc-en-ciel [11];
- Pour =
x y
a a
, on retrouve le cas particulier de la sphère traité par Marston [2,3] avec
(
)
(
)
γ
α α θ = = −1/ cos
Sphère x C
a [12];
- Pour ≠
x y
a a
l’expression obtenue pour
γ
α
est bien plus complexe mais, après quelques
calculs [12], on peut montrer elle est identique à celle d’une sphère dont le rayon est égal
au rayon de courbure, du sphéroïde 2D, au niveau du paramètre d’impact critique :
(
)
γ
α α = = = =
2 2
3
Sphère x y c x y
c
R a aa
N
a ! Ceci est illustré numériquement par la figure 3 qui compare
la forme du front d’onde diffracté par des bulles sphéroïdales et sphériques (de rayon
=
x
a a
et
=
y
a a
ainsi que =
c
a R
pour le cas oblate et le cas prolate).

13
ième
Congrès Francophone de Techniques Laser, CFTL 2012 - ROUEN, 18 – 21 Septembre 2012
La seconde étape porte sur l’étude de la propagation dans le champ lointain de ce front
d'onde. En conservant les notations utilisées par Marston [2] dans le cas de la sphère, nous
utilisons comme expression générique de l'amplitude du champ diffusé au voisinage de l’angle
critique :
( ) ( )
(
)
α η
η
∞− −
−∞
=
∫
2
ik u u
j j
f r u e du
(6)
où
η φ φ
= −
c
est un écart angulaire infinitésimal et
j
r
est une approximation au premier ordre de
l'amplitude du coefficient de Fresnel
(
)
=
1,2
j avec
k
pour le vecteur d’onde et
c
0
ε θ θ
= − ≥
avec
( )
( )
ε θ −≃
1/2
1
1 8 / cos
c
r m et
( )
( )
ε θ ≈ − +
1/2
2
2
1 8 / cos
c
r m m [12]. En remplaçant, il vient que :
( )
η
ηα β
α
α
η
− + +
∞ 
−∞
= ±
∫
2
21/2
2
4
j
ki k u u
i
j
f e e du
(7)
Pour obtenir une intégrale formellement identique à celle Fresnel, nous introduisons deux
nouvelles constantes
A
et
w
:
αη
π πα
− −
= = −
2
; 2
k k
A w (8)
Après quelques manipulations [12], l’Eq. (7) devient :
( )
( )
β
ηβ β
π
α
η
− 
  − + −
− −
∞   
−
= ±
∫
21/2 1/2 1/2
1/2 21/2 1/2
42
jj j
k
i i w i z w w
Ai z A A
jw
e
f e e dz
A
(9)
On introduit alors la fonction
( ) ( )
β
ψ
= + −
1/2
1/2
1/2
,
j
j
z w z w w
A
. Selon la méthode des phases
stationnaires, le terme
( )
ψ −
,
j
i z w
e , qui oscille rapidement pour les grosses bulles, est négligeable. On
a donc que
( ) ( )
β
ψ ψ
→ → = =
1/2
1/2
, 0 ,0
j
j j
z w w w w
A
. En se limitant au domaine φ φ
−
−
∼
0
c
et en introduisant
une fonction d’amplitude
g
telle que
( ) ( )
1
j
f g
A
η η
= ± , on obtient pour la fonction d’amplitude du
champ diffusé :
( )
( ) ( )
2
2
,0
4 , 2
jj
k
i w i z
i z w
w
g e e e dz
ηπ
ψ
α ψ
η
−
− −
∞
−
−
=
∫
(10)
Finalement, en écrivant le vecteur de Poynting et en omettant le terme de décroissance en
1/r
2
de l’énergie, on trouve que la diffusion d’une bulle oblate ou prolate peut être décrite à l'aide
des intégrales de Fresnel [2, 4, 12]:
( )
( ) ( )
θ π π ∝ + + +
∫ ∫
2 2
2 2
0 0
cos / 2 1/ 2 sin / 2 1/ 2 ,
w w
I z dz z dz (11)
Cette dernière expression dépend de λ
1 2
, / , ,
x y
m m a a
à travers
η πα
= − − / 2w k . Les extrema de
(
)
θ
I
correspondent aux franges (anneaux) brillant(e)s et sombres généré(e)s par la diffusion critique
[4].
En guise d’illustration, la figure 4 compare l’évolution des diagrammes de diffusion au voisinage de
l’angle critique de bulles sphéroïdales 2D (ou jets) : (a) POA-sphéroïde, (b) TLM pour un cylindre
dont le rayon est égal au rayon de courbure du sphéroïde au niveau du paramètre d’impact
critique. Une rotation est simulée de façon à modéliser la rotation du diffuseur ou, plus simplement,
de façon à balayer différents rayons (de courbure). La figure 4 (a) compare également la position
des franges principales (en bleu : POA sphéroïde ; en rouge : TLM & rayon de courbure). L’accord
est globalement bon. Le décalage angulaire des franges (ou anneaux), entre POA-sphéroïde et
LMT-rayon de courbure, est tout à fait comparable à ce que l’on obtient avec une sphère [2,4-5]. Il

13
ième
Congrès Francophone de Techniques Laser, CFTL 2012 - ROUEN, 18 – 21 Septembre 2012
ne s’agit donc pas d’un artefact du modèle introduit ici. Ce décalage indique simplement qu’il faut
prendre en compte d’autres phénomènes optiques (les rayons p>1 notamment) [3,5].
3 Tests expérimentaux
Une expérience a été développée dans le but de valider le modèle précédemment établi. Celle-ci
repose sur l'enregistrement et l’analyse, à l'aide d'un montage de diffraction, de la diffusion critique
générée par des jets capillaires de section elliptique. Ces jets sont produits au moyen d’un
capillaire de section elliptique dont l’orientation est contrôlée par un goniomètre. Le jet est lui-
même composé d’huile silicone (RHODORSIL® 47 V 20) injectée à
≈
1 m/s dans de l’eau. Le
reste de l’expérience : faisceau laser (source, fibre, polariseur et agrandisseur de faisceau), cuve
d’analyse, système de détection (lentille de collection, filtrage spatial, diaphragme, filtre
interférentiel et lentille de Fourier) et système de µvidéo (source, fibre, lentille de collimation,
objectif et caméra) sont identiques à ceux décrits dans nos précédents travaux [8-9]. Une petite
différence néanmoins : une lentille cylindrique est ajoutée au système d’émission CARS pour
éclairer le jet avec une feuille laser
(
)
ω ω ≈ ≈
0 0
2 20 ,2 20
z y
µm mm
perpendiculaire à l’axe du jet.
La figure 5 montre une photographie d’une partie du dispositif, de même que deux photographies
d’un jet et de son diagramme de diffusion critique (observé sur une feuille de papier placée à cet
effet devant la détection CARS).
Pour un débit constant, le jet adopte une forme elliptique qui évolue axialement entre une
configuration prolate et oblate. Pour pouvoir comparer les analyses µvidéo et CARS, ces systèmes
n’observant pas le jet sous le même angle, il faut ajuster l’orientation du capillaire à l’aide du
goniomètre. Nous notons β
v
cet angle ou écart angulaire, voir la figure 2. La figure 6 montre
l’analyse µvidéo du profil d’un jet lorsque le grand-axe du capillaire est orienté le long ou
perpendiculairement à l’axe optique du système µvidéo. On constate que l’ellipticité du jet décroit
fortement en fonction de la distance axiale, avec des maxima et minima successifs
(correspondants à des jets de section alternativement prolate, oblate, prolate,…). De même, en
sortie immédiate du capillaire, on remarque que la très forte contraction du jet s’attenue après une
à deux oscillations (la courbure locale suivant la direction axiale est beaucoup plus modérée :
condition sine qua non pour valider notre modèle 2D). Nos mesures CARS (avec une feuille laser
de faible hauteur) ont donc été effectuées au niveau du ventre de la deuxième oscillation.
A partir des images µvidéo, on peut déterminer, pour une distance axiale et un angle d’orientation
donnés : un diamètre ou plus exactement une « corde » du jet (voir la figure 2). Pour un jet de
section elliptique, il existe une relation mathématique directe entre cette corde L
c
et l’angle
d’orientation du jet par rapport à l’axe optique des deux systèmes optiques. Celle-ci dépend
également des deux extrema (grand axe et petit axe de l’ellipsoïde présupposé). La figure 7
compare l’évolution théorique de cette corde avec celle obtenue expérimentalement pour un
intervalle de 0 à 180°. L’accord est plutôt bon, même si le profil du jet n’est pas parfaitement
elliptique.
Comme pour la figure 4 (a), la figure 8 (a) montre l’évolution simulée pour le diagramme de
diffusion d’un jet en fonction de l’angle de rotation. La Error! Reference source not found. (b)
montre le résultat expérimental correspondant. Si les comportements globaux sont assez
similaires, nous remarquons des différences notables (surtout pour les angles intermédiaires).
Nous attribuons celles-ci aux contributions des rayons
1
p
≥
qui ne sont pas prises en compte dans

13
ième
Congrès Francophone de Techniques Laser, CFTL 2012 - ROUEN, 18 – 21 Septembre 2012
le modèle actuel. Les écarts observés ici ne sont donc pas totalement surprenants. De nouvelles
expériences sont néanmoins en cours.
4 Conclusion
Nous avons présenté les premiers résultats théoriques d’un modèle permettant de décrire, dans le
cadre de l’optique physique, la diffusion d’une bulle sphéroïdale 2D (elliptique) au voisinage de
l’angle critique. Les résultats de ce modèle sont en bon accord avec ceux obtenus avec la théorie
de Lorenz-Mie même si, pour une description plus détaillée, nous devrons à terme prendre en
compte les contributions des rayons simplement ou multiplement réfractés. Les comparaisons
expérimentales confirment les conclusions tirées des résultats numériques.
Les auteurs tiennent à remercier pour leur soutien le « Bulgarian National Scientific Fund » via le
projet DO 02-338/2008 et l’ANR pour le projet CARMINA-ANR-09-BLAN-0023-01.
5 Références
[1] Fiedler-Ferrari N., Nussenzweig H.M., and Wiscombe W.J., "Theory of near-critical-angle scattering from
a curved interface," Phys. Rev. A 43, 1005-1038 (1991).
[2] Marston P.L., "Critical scattering angle by a bubble: physical optics approximation and observations,"
JOSA A 69, 1205-1211 (1979).
[3] Langley D.S., and Marston P. L., "Critical scattering of laser light from bubbles in water: measurements,
models, and application to sizing bubbles " Appl. Opt. 23, 1044-1054 (1984).
[4] Onofri F., "Critical Angle Refractometry: for simultaneous measurement of particles in flow size and
relative refractive index," Part. and Part. Syst. Charact. 13, 119-127 (1999).
[5] Onofri F.R.A., Krzysiek M., Mroczka J., Ren K-F., Radev St., and Bonnet J-P., "Optical characterization
of bubbly flows with a near-critical-angle scattering technique," Exp. in Fluids 47, 721-732 (2009).
[6] Davis G.E., "Scattering of light by an air bubble in water," JOSA A 45, 572-581 (1955).
[7] Lock J.A., "Role of the tunneling ray in near-critical-angle scattering by a dielectric sphere," JOSA A 20,
499-507 (2003).
[8] Onofri F., Krzysiek M., and Mroczka J., "Critical Angle Refractometry and Sizing for Bubbly Flow
Characterization," Opt. Lett. 32, 2070 (2007).
[9] Onofri F.R.A., Krzysiek M.A., Barbosa S., and Mroczka J., "Critical Angle Refractometry and Sizing
technique for bubbly flows characterization: Particular effects," App. Opt. 50(30) :5759-5769 (2011)
[10] Grace J.R., Wairegi Т., and Nguyen Т.Н., "Shapes and velocities of single drops and bubbles moving
freely through immiscible liquids," Trans. Inst. Chem. Eng. 54, 167-173 (1976).
[11] Airy G. B., "On the intensity of light in the neighbourhood of a caustic," Transactions of the Cambridge
Philosophical Society 6, 397-403 (1838)
[12] Onofri F. Radev S., Physical-optics approximation of the near-critical-angle scattering of 2D spheroidal
bubbles, rapport interne, IUSTI UMR 7343, Marseille, France (2011).