Ex5

TD MECANIQUE Correction
Exercice 5 : Voyage Terre – Mars
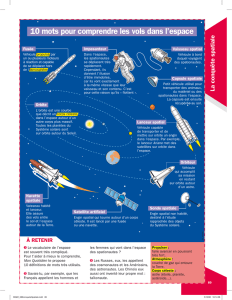
1. Sur l’orbite de transfert de Hohmann d’excentricité eet le paramètre p,r=p
1+ecos θ,
S T
A
M
α
V
θ
Au périgée, Tsur la figure, θ= 0 et alors r=rT=p
1+e.
De même à l’apogée, θ=π,r=rM=p
1−e. On en déduit
rT
rM
=1−e
1 + e⇒e=rM−rT rM+rT
= 0,21 ⇒p=rT(1 + e) = 182.106km.
2. Lors du voyage, le vaisseau parcourt la moitié de l’ellipse donc sa durée τcorrespond à une
demi période THdu vaisseau sur l’orbite de Hohmann.
Et, d’après la troisième loi de Kepler,
T2
a3Terre
=T2
a3Hohmann
⇒T2
T
r3
T
=4τ2
(rT+rM
2)3⇒τ=1
2rT+rM 2rT3
2
TT≃0,71TT
où TTest la période de révolution de la Terre autour du soleil (1 an). On en déduit τ≃8 mois
et 20 jours.
3. Le vaisseau étant dans un état lié (trajectoire circulaire ou elliptique),
Em=−k
2a=Ec+Ep=1 2mv2−k r⇒v=s2k m1 r−1 2a=s2GMS1 r−1 2a
Au voisinage de la Terre, sur l’orbite circulaire c’est à dire avant l’allumage des moteurs r=
rT=ad’où v(T−) = q2GMS
rTpuis toujours en r=RTmais sur l’orbite elliptique 2a=rT+rM
d’où v(T+) = q2GMS[1
rT−1 rT+rM].
On en déduit au niveau de la Terre ∆vT=qGMS
rT(q2rM rT+rM−1) ≃3km.s−1.
Aux environs de Mars par le même type de calculs, ∆vM=qGMS
rM(1−q2rT rT+rM)≃ −2,7km.s−1
4. Dans le cas d’un mouvement circulaire de rayon Em=−k
2a=−GMSm 2rd’où
∆Em=Em(M)−Em(T) = −GMSm
r(1 rM
−1
rT
) = 1
2GmMS
rM−rT
rMrT
≃1,55.1011 J.
5. Pour ne pas manquer le rendez-vous, il faut que Mse situe en Aau même instant que V, c’est
à dire à t=τ.
Métant animé d’un mouvement circulaire uniforme, sa vitesse angulaire est 2π
TM=π−α τavec
d’après la troisième loi de Kepler,
T2
M
r3
M
=T2
T
r3
T
⇒TH=TTrM
rT3
2⇒α=π1−2τ
TT
(rT
rM
)3
2≃45,3˚
1