ME6_Poly_Lois de Képler

Le système solaire
Le système solaireLe système solaire
Le système solaire :
::
:
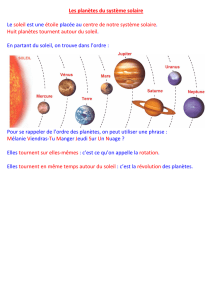
Une étoile (soleil) + 8 planètes
 Masse SOLEIL :
30
2 10≈ ⋅
S
m kg
 Masse TERRE :
24
6 10≈ ⋅
T
m kg
 Masse JUPITER :
27
320 2 10≈ ≈ ⋅
J T
m m kg
(La plus lourde du système solaire)
Conséquences :
 La masse des planètes est négligeable devant celle du soleil
 Le soleil peut être considéré comme immobile (Faible influence des planètes sur sa position)
 On peu considérer que chaque planète n’est soumise qu’à 1 force centrale (Gravitation du soleil)
Trois l
Trois lTrois l
Trois lois de Képler
ois de Képlerois de Képler
ois de Képler :
::
:
Képler a formulé les lois du mouvement des planètes du système solaire à partir de ses observations (et celles de Tycho-Brahé)
a)
a) a)
a) Première loi (1605)
Première loi (1605)Première loi (1605)
Première loi (1605) :
::
: les trajectoires des planètes sont des ellipses dont le soleil occupe l’un des foyers.
b)
b) b)
b) Seconde loi (1604)
Seconde loi (1604)Seconde loi (1604)
Seconde loi (1604) :
::
: le rayon vecteur Soleil - Planète balaye des aires égales en des temps égaux.
c)
c) c)
c) Troisième loi (1618)
Troisième loi (1618)Troisième loi (1618)
Troisième loi (1618) :
::
: le carré de la période orbitale T des planètes est proportionnel au cube du grand
axe de leur ellipse :
2 2
3
4
TCstte
a GM
π
= =
Justification :
a)
a)a)
a) Force newtonienne (Centrale + Conservative + en 1/r
2
)  Mouvement plan, elliptique, parabolique ou hyperbolique
b)
b)b)
b) Force Centrale  Loi des aires (Obtenue par observation en 1600 !!!)
c)
c)c)
c) Troisième loi : exprime le caractère constant de la vitesse aréolaire (Voir démonstration dans le cas circulaire)
Cas particulier du mouvement circulaire
Cas particulier du mouvement circulaireCas particulier du mouvement circulaire
Cas particulier du mouvement circulaire :
::
:
Etude
Etude Etude
Etude énergétique
énergétiqueénergétique
énergétique :
::
:
Etudions le cas particulier d’un mouvement circulaire de rayon R :
0
θ θ
= =
ɺ
ɺ ɺ
POL POL
r
vr R
et
2
2
θ
θθ
  −
−
= =
ɺ
ɺɺ ɺɺ
POL
POL
v
RR
aRR
Energie potentielle : Force gravitationnelle
2
= − ⋅ ⇒= −
r P
GMm GMm
f e E
r r
Energie cinétique :
2 2
1 1
2 2
θ
= =
C
E mv mv
(vitesse radiale nulle)
PFD pour relier les
PFD pour relier les PFD pour relier les
PFD pour relier les 2
22
2 :
::
:
2
2
2
1 1
2 2 2
0
θ
  −
−−
= = = ⇒=== ⇒= =
ɺɺ
C P
mv
GMm
GMm GM
f ma E mv E v cstte
R
R
R R
mR
Démonstration de la
Démonstration de la Démonstration de la
Démonstration de la 3
33
3
ème
èmeème
ème
loi de Képler dans le cas d
loi de Képler dans le cas dloi de Képler dans le cas d
loi de Képler dans le cas d’
’’
’une orbite circulaire
une orbite circulaireune orbite circulaire
une orbite circulaire :
::
:
 Constante des aires :
2
GM
C R Rv R RGM
R
θ = = = =
ɺ
 Loi des aires :
2
1
2 2
dA C
r
dt
θ
= =
ɺ
, et en intégrant :
2
2
disque
C
A T R
π
= =
CH16
CH16 CH16
CH16
–
––
–
TMC
TMC TMC
TMC
:
::
:
V.1
V.1V.1
V.1
)
) )
)
Lois de Képler
Lois de KéplerLois de Képler
Lois de Képler
V.2)
V.2) V.2)
V.2)
Cas particulier du mouvement circulaire
Cas particulier du mouvement circulaireCas particulier du mouvement circulaire
Cas particulier du mouvement circulaire
2 2
3
4T
Cstte
R GM
π
⇒= =
Cette loi se généralise au cas elliptique en prenant R = a :
2 2
3
4 π
⇒= =
T
Cstte
a GM