5G2 - Angles

5G2 - Angles
0] Rappels
0.1. Vocabulaire
Le sommet de l'angle
ACB
est le point C ;
Ses côtés sont les demi-droites [CA) et [CB).
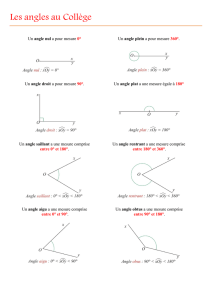
Angle nul Angle aigu Angle droit Angle obtus Angle plat
0.2. Angles adjacents
Deux angles sont adjacents si :
a) ils ont le même sommet ;
b) ils ont un côté commun ;
c) ils sont situés de part et d'autre de ce côté commun.
0.3. Bissectrice d'un angle
Définition Propriété
La bissectrice d'un angle est la demi-droite
qui partage cet angle en deux angles adjacents de
même mesure.
La bissectrice d'un angle est l'axe de symétrie de cet
angle.
1] Vocabulaire
1.1. Angles complémentaires et supplémentaires
On dit que deux angles sont complémentaires lorsque leur somme est égale à 90°.
On dit que deux angles sont supplémentaires lorsque leur somme est égale à 180°.
Exemples :
Paire d'angles complémentaires Paire d'angles supplémentaires
1.2. Angles opposés par le sommet
Définition Figure Propriété
On dit que deux angles sont opposés par le
sommet lorsqu'ils ont le même sommet et que leurs
côtés sont dans le prolongement l'un de l'autre.
Si deux angles sont opposés par
le sommet, alors ils sont de
même mesure.
C
A
B
0° 0° < Â < 90° 90° 90° < Â < 180°
Sommet
commun Côté
commun
180°
34°
56°
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( 0.64 , -1.84 ) { i };
51°
129°
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( 0.81 , -2.06 ) { i };
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( -2.97 , -1.52 ) { i };

5G2 - Angles (fin)
2] Propriétés
2.1. Angles alternes-internes et angles correspondants
Paire d'angle alternes-internes Paire d'angles correspondants
Si deux droites parallèles sont coupées par
une sécante, alors les angles alternes-internes
qu'elles déterminent sont égaux.
Si deux droites parallèles sont coupées par
une sécante, alors les angles correspondants
qu'elles déterminent sont égaux.
Figure : Figure :
2.2. Prouver que deux droites sont parallèles...
... avec une paire d'angle alternes-internes ... avec une paire d'angles correspondants
Si deux droites sont coupées par une sécante en
formant une paire d'angles alternes-internes égaux,
alors ces deux droites sont parallèles.
Si deux droites sont coupées par une sécante en
formant une paire d'angles correspondants égaux,
alors ces deux droites sont parallèles.
Figure : Figure :
3] Somme des angles d'un triangle
La somme des angles
d'un triangle est égale à 180°.
Exercice :
Soit ABC un triangle tel que
ABC=65 °
et
BAC=20°
.
Calculer la mesure de l'angle
ACB
.
ACB=180°− ABC  BAC 
ACB=180°−65°20 °
ACB=180°−85°
ACB=95°
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( -2.79 , -1.88 ) { i };
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( -3.14 , -1.81 ) { i };
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( -2.79 , -1.88 ) { i };
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( -2.15 , -0.42 ) { i };
A
B
C
65°
20°
95°
@options;
repereortho(313,263,30,1,1){ 0 ,
moyen , noir , num1 ,i};
@figure;
A = point( 3.56 , 1.97 ) { car-2 ,