suivante - Fabrice Rossi

L2/L3 MASS/MIAGE Année universitaire 2013 – 2014
Université Paris 1
Aide mémoire pour le cours de mathématiques pour l’informatique
Fabrice Rossi
1 Automates et langages rationnels
1.1 Notations et définitions
– on note en général Σl’alphabet considéré, un ensemble fini de symboles (souvent a,b,c, . . .) ;
– si Σest un alphabet, on note Σ
∗
l’ensemble de tous les mots formés des symboles de Σ, en incluant
notamment le mot vide ε;
– le nombre de symboles d’un mot w∈Σ∗est sa longueur, notée |w|;
– si Let Msont des langages (des sous-ensembles de Σ∗) :
–L.M =LM est l’ensemble des mots constitués d’un mot de Lsuivi d’un mot de M;
–L|M = L∪M est l’union des langages, c’est-à-dire l’ensemble des mots soit dans L soit dans
M;
– si Lest un langage, on note :
–L0={ε};
–L1=L;
–L? = L|L0;
–Lk+1 =L.Lk=Lk.L ;
–L+=Sk≥1Lk;
–L∗=Sk≥0Lk.
– pour tout mot w∈ Σ
∗
, on note par simplification w le langage réduit au mot w seul, c’est-à-dire
le langage L={w};
– un langage L sur Σest rationnel (ou régulier) si et seulement si soit il est vide L = ∅ , soit il
vérifie une des conditions suivantes :
1. L={ε};
2. L={a}pour un symbole a∈Σ;
3. L=L1|L2pour deux langages rationnels L1et L2;
4. L=L1L2pour deux langages rationnels L1et L2;
5. L=L∗
1pour un langage rationnel L1.
1.2 Résultats théoriques
1.2.1 Lemme de Arden
Soit αet βdeux langages sur l’alphabet Σ. Si ε6∈ α, alors le seul langage Xqui vérifie
X=αX|β
est X=α∗β.
1.2.2 Lemme de l’étoile
Soit L un langage rationnel sur Σ. Il existe un entier N ne dépendant que de L tel que tout mot
w∈L de longueur |w| ≥ N possède une décomposition sous la forme w = xyz vérifiant les propriétés
suivantes :
1

1. 0<|y| ≤ N;
2. pour tout n > 0,xynz∈L.
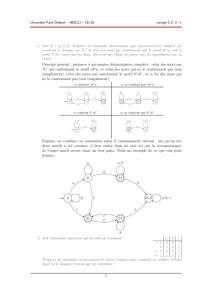
1.3 Algorithme de Thompson
L’algorithme de Thompson construit à partir d’un langage rationnel non vide un automate (en
général non déterministe) qui le reconnaît. La construction garantit que l’automate obtenu a un unique
état terminal distinct de son état initial. Elle fonctionne récursivement à partir de la définition des
langages rationnels rappelée ci-dessus. Dans les schémas qui suivent, les flèches ondulées résument un
automate complet reconnaissant le langage indiqué au dessus de la flèche. L’état ik était l’état initial de
l’automate reconnaissant Lk et l’état fk était son état final. Pour le langage L , l’état initial est noté i
et l’état final f.
Soit Lrationnel non vide, alors une des conditions suivantes est vraie :
1. si L={ε}, l’algorithme construit l’automate :
if
ε
2. si L={a}, l’algorithme construit l’automate :
if
a
3. si L = L1|L2 , l’algorithme construit récursivement un automate pour L1 et un automate pour L2 ,
puis les combine en :
i
i1
i2
f1
f2
f
ε
ε
ε
ε
L1
L2
4. si L = L1L2 , l’algorithme construit récursivement un automate pour L1 et un automate pour L2 ,
puis les combine en :
i=i1f1/i2f=f2
L1L2
L’état f1/i2 est la fusion de l’état final de l’automate reconnaissant L1 avec l’état initial de
l’automate reconnaissant L2.
5. si L = L∗
1
, l’algorithme construit récursivement un automate pour L1 puis construit l’automate
suivant :
ii1f1f
ε ε
ε
ε
L2
2

2 Calcul propositionnel
2.1 Formules
Les formules de la logique propositionnelle sont construites à partir :
– d’un ensemble fini de variables propositionnelles, V (en général des lettres minuscules, par exemple
V={a, b, c}) ;
– d’un opérateur unaire de négation ¬;
– de quatre opérateurs binaires :
1. ou : ∨;
2. et : ∧;
3. implique : ⇒;
4. équivalent : ⇔.
On note F(V)l’ensemble des formules construites sur les variables propositionnelles V.
2.2 Notations
– on utilise souvent deux constantes : > dont la valuation est toujours 1 et ⊥ dont la valuation est
toujours 0 ;
– on note F≡G si et seulement si pour toute valuation v , v ( F ) = v ( G )(les formules F et G sont
sémantiquement équivalentes).
2.3 Équivalences notables
Si cela est indiqué dans l’énoncé, on peut utiliser les équivalences notables suivantes pour simplifier
ou transformer des formules :
(X⇒Y)≡((¬X)∨Y) (X⇔Y)≡((X⇒Y)∧(Y⇒X))
((X∧Y)∧Z)≡(X∧(Y∧Z)) ((X∨Y)∨Z)≡(X∨(Y∨Z))
(X∧Y)≡(Y∧X) (X∨Y)≡(Y∨X)
(X∧(Y∨Z)) ≡(X∧Y)∨(X∧Z)) (X∨(Y∧Z)) ≡(X∨Y)∧(X∨Z))
(¬(¬X)) ≡X
(¬(X∧Y)) ≡((¬X)∨(¬Y) (¬(X∨Y)) ≡((¬X)∧(¬Y)
2.4 Règles de Quine
Dans l’algorithme de Quine, on utilise les équivalences notables suivantes :
(¬⊥)≡ > (¬>)≡ ⊥
(> ⇒ X)≡X(X⇒ >)≡ >
(⊥ ⇒ X)≡ > (X⇒ ⊥)≡(¬X)
(X∨ >)≡ > (X∨ ⊥)≡X
(> ∨ X)≡ > (⊥ ∨ X)≡X
(X∧ >)≡X(X∧ ⊥)≡ ⊥
(> ∧ X)≡X(⊥ ∧ X)≡ ⊥
(X⇔ >)≡X(X⇔ ⊥)≡(¬X)
(> ⇔ X)≡X(⊥ ⇔ X)≡(¬X)
3

2.5 Calcul des séquents
Le calcul des séquents repose (exclusivement) sur huit règles (sauf mention contraire, on n’utilise
pas les équivalences notables) :
Γ,A,B,∆`Θ∧g
Γ,(A∧B),∆`Θ
Θ`Γ,A,∆ Θ `Γ,B,∆∧d
Θ`Γ,(A∧B),∆
Γ,A,∆`Θ Γ,B,∆`Θ∨g
Γ,(A∨B),∆`Θ
Θ`Γ,A,B,∆∨d
Θ`Γ,(A∨B),∆
Γ,∆`A,Θ Γ,B,∆`Θ⇒g
Γ,(A⇒B),∆`Θ
A,Γ`∆, B, Θ⇒d
Γ`∆,(A⇒B),Θ
Γ,∆`A,Θ¬g
Γ,(¬A),∆`Θ
A,Γ`∆,Θ¬d
Γ`∆,(¬A),Θ
On admet comme axiomes les séquents de la forme suivante :
Γ,A `Θ,A
où Adésigne une formule (on ne limite pas Aà être une variable propositionnelle).
3 Logique de Hoare
3.1 Interprétation
Sauf mention contraire explicite, on suppose en général que l’interprétation des symboles de fonctions,
des symboles de constantes et des symboles de prédicats est celle de l’arithmétique dans Z . En particulier,
le symbole / désigne la division euclidienne, c’est-à-dire que 5 / 2est le quotient de la division de 5par 2
(soit 2). Le symbole %correspond au calcul du reste de la division (par exemple 5%2 = 1).
3.2 Notations
On rappelle que dans les triplets de Hoare, les accolades {} sont utilisées pour la correction partielle
(on ne considère que les cas où le programme s’arrête) alors que les crochets hi sont utilisés pour la
correction totale (le programme doit toujours s’arrêter).
Si F est un terme (resp. une formule) du calcul des prédicats, F [ x←T ]est le terme obtenu (resp.
la formule obtenue) en remplaçant toutes les occurrences libres de x par T . Si on autorise les variables
booléennes, Tpeut être une formule, sinon Test un terme.
3.2.1 Logique de Hoare
La logique de Hoare repose sur des règles de déduction et des axiomes. Les axiomes sont ceux de
l’affectation (Hoare et Floyd) :
←Hoare
hF[x←T]ix←ThFi
Dans l’axiome ci-dessus, il faut que xsoit une variable libre dans F.
←Floyd
hFix←Th(∃y, (F[x←y]∧(x=T[x←y])))i
Le reste du système consiste en les règles de déduction suivantes :
hFiprog1 hGi hGiprog2 hHi;
hFiprog1; prog2 hHi
4

(F⇒G)hGiprog hHi(H⇒I)⇒
hFiprog hIi
h(F∧b)iprog1 hGi h(F∧(¬b))iprog2 hGiif then
hFiif (b) prog1 else prog2 end if hGi
{(I∧b)}prog {I}while partiel
{I}while(b) prog end while {(I∧(¬b))}
Dans la règle précédente, Iest appelé invariant de la boucle.
h(I∧b∧(V=n))iprog hI∧(V < n)∧(V≥0))iwhile total
hIiwhile(b) prog end while h(I∧(¬b))i
Dans cette dernière règle, V est un terme et n une variable libre qui n’est utilisée nulle part ailleurs.
Comme dans la règle précédente, Iest un invariant, alors que Vest un variant de la boucle.
5