Calcul d`un terme de rang donné

Calcul d’un terme de rang donné
Suite arithmétique
Un petit village de Chine surveille avec
inquiétude l’avancée d’une dune de sable de
plusieurs km de long. Elle n’est plus
aujourd’hui en 2011 qu’à 200m des
premières maisons du village et avance à
une vitesse moyenne de 10m/an.
Pour n  0 , on note dn la distance en
séparant le village de la dune. On suppose
que la dune continue d’avancer à la même
allure.
Calculer la distance séparant la dune du
village dans 12 ans.
On a :
Premier Terme : d0 = 200;
Terme Général: dn = 200 – 10n ;
Terme Récurrent : d n+1 = dn – 10 ;
Suite géométrique
Une balle élastique est lâchée d’une hauteur
de 100m au dessus du sol. La hauteur
atteinte à chaque rebond est égale à 9
10 de la
hauteur du précédent.
Calculer la hauteur, en cm près, du dixième
rebond.
On a :
Premier Terme : U0 =100
Terme Général : U n+1 = 9
10 Un
Terme Récurrent : Un = 100 × 9
10 
Utilisation de la forme explicite
Utilisation de la forme explicite
Programme nom_du_programme ;
VAR U : réel ;
N : entier ;
DEBUTPROG
Afficher("hauteur de départ") ;
Saisir(U) ;
Afficher("nombre de rebond voulu") ;
Saisir(N) ;
U <- U*puissance((9/10),N);
Afficher("la hauteur au",N,"ième
rebond est",U) ;
FINPROG

Utilisation de la relation de récurrence
Programme nom_du_programme ;
VAR D : réel ;
N : entier ;
index : entier ;
DEBUTPROG
Afficher("distance du village
en 2011" ) ;
Saisir (D) ;
Afficher ("année voulue") ;
Saisir (N) ;
POUR index <- 0 JUSQU'A N
FAIRE
D <- D-10 ;
FINP
Afficher{ "la distance
séparant la dune du village
dans",n,"ans est",D } ;
FINPROG
Utilisation de la relation de récurrence

Exercice suites : Intérêts simples, intérêts composés
Une personne souhaite placer durant plusieurs années un capital de 20 000 euros.
Elle hésite entre deux types de placements :
 Un placement à intérêts simples à 2,25 % l’an : chaque année, son capital augmente d’une
somme fixe égal à 2,25 % du capital initial, c’est-à-dire de 450 € ;
 Un placement à intérêts composés à 2 % l’an : dans ce cas, les intérêts produits sont
capitalisés, et rapportent donc eux aussi 2 % l’an.
On désigne par Sn le capital obtenu au terme de n années lorsque les intérêts sont simples
(S0 = 20 000), et Cn le capital obtenu au terme de n années lorsque les intérêts sont composés
(C0 = 20 000).
1°) Calculer S1 et C1.
2°) Quelle est la nature de la suite (Sn) ? De la suite (Cn) ? Justifier.
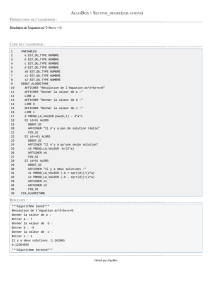
3°) Faire fonctionner l’algorithme ci-dessous qui détermine le terme de rang n de chacune des
deux suites, et qui donne le placement le plus avantageux suivant la valeur de n.
1 VARIABLES
2 n EST_DU_TYPE NOMBRE
3 i EST_DU_TYPE NOMBRE
4 S EST_DU_TYPE LISTE
5 C EST_DU_TYPE LISTE
6 DEBUT_ALGORITHME
7 LIRE n
8 S[0] PREND_LA_VALEUR 20000
9 C[0] PREND_LA_VALEUR 20000
10 POUR i ALLANT_DE 0 A n
11 DEBUT_POUR
12 S[i+1] PREND_LA_VALEUR S[i]+450
13 C[i+1] PREND_LA_VALEUR C[i]*1.02
14 FIN_POUR
15 SI (S[n]>C[n]) ALORS
16 DEBUT_SI
17 AFFICHER "le placement 1 est le plus avantageux"
18 FIN_SI
19 SINON
20 DEBUT_SINON
21 AFFICHER "le placement 2 est le plus avantageux"
22 FIN_SINON
23 AFFICHER "S[n] = "
24 AFFICHER S[n]
25 AFFICHER "C[n]="
26 AFFICHER C[n]
27 FIN_ALGORITHME

0
5000
10000
15000
20000
25000
30000
35000
40000
1
3
5
7
9
11
13
15
17
19
21
23
25
Série2
Série3
Série4
Comparaison du comportement de différentes suites
Dans une grande ville, 3 opérateurs téléphoniques proposent des abonnements renouvelables
chaque trimestre. On suppose que les tendances observées vont se maintenir quelques années.
 Opérateur 1 Osanguine : 8000 abonnés initialement et 500 nouveaux recrutés chaque
trimestre
 Opérateur 2 Cé pa fèr : 5000 abonnés initialement et croissance de 8% du nombre
d’abonnés chaque trimestre
 Opérateur 3 BEUG: 10000 abonnés initialement, un taux de réabonnement trimestriel
de 80% et 2500 nouveaux recrutés chaque trimestre.
Au bout de 2 ans, quel opérateur a le plus d’abonnés ?
Au bout de 3 ans, quel opérateur a le plus d’abonnés ?
Au bout de 5 ans, quel opérateur a le plus d’abonnés ?
Solution :
 Opérateur 1 : U0 = 8000 et U n+1 = Un + 500
 Opérateur 2 : V0=5000 et V n+1 = 1,08 Vn
 Opérateur 3 : W0=10000 et W n+1 = 0,8 Wn + 2500
Avec un tableur
série 2
série 3
série 4
n
Un
Vn
WN
0
8000
5000
10000
1
8500
5400
10500
2
9000
5832
10900
3
9500
6298,56
11220
4
10000
6802,4448
11476
5
10500
7346,64038
11680,8
6
11000
7934,37161
11844,64
7
11500
8569,12134
11975,712
8
12000
9254,65105
12080,5696
9
12500
9995,02314
12164,4557
10
13000
10794,625
12231,5645
11
13500
11658,195
12285,2516
12
14000
12590,8506
12328,2013
13
14500
13598,1186
12362,561
14
15000
14685,9681
12390,0488
15
15500
15860,8456
12412,0391
16
16000
17129,7132
12429,6313
17
16500
18500,0903
12443,705
18
17000
19980,0975
12454,964
19
17500
21578,5053
12463,9712
20
18000
23304,7857
12471,177

Comparaison_evolution_suites – Version algobox
1 VARIABLES
2 O EST_DU_TYPE NOMBRE
3 C EST_DU_TYPE NOMBRE
4 B EST_DU_TYPE NOMBRE
5 i EST_DU_TYPE NOMBRE
6 N EST_DU_TYPE NOMBRE
7 DEBUT_ALGORITHME
8 AFFICHER "Nombre d'abonnés initialement à
Sanguine "
9 LIRE O
10 AFFICHER "Nombre d'abonnés initialement à
Cé pa Fèr "
11 LIRE C
12 AFFICHER "Le nombre d'abonnés initialement
à BEUG "
13 LIRE B
14 AFFICHER "Nombre de trimestres voulus "
15 LIRE N
16 POUR i ALLANT_DE 1 A N
17 DEBUT_POUR
18 O PREND_LA_VALEUR O+500
19 C PREND_LA_VALEUR 1.08*C
20 B PREND_LA_VALEUR 0.8*B+2500
21 FIN_POUR
22 SI (O>C) ALORS
23 DEBUT_SI
24 SI (B>O) ALORS
25 DEBUT_SI
26 AFFICHER "Beug a le plus d'abonnés en "
27 AFFICHER N
28 AFFICHER "Trimestres. le nombre
d'abonnés est "
29 AFFICHER B
30 FIN_SI
31 SINON
32 DEBUT_SINON
33 AFFICHER "Sanguine a le plus d'abonnés en "
34 AFFICHER N
35 AFFICHER "trimestres. le nombre d'abonnés
est "
36 AFFICHER O
37 FIN_SINON
38 FIN_SI
39 SINON
40 DEBUT_SINON
41 SI (B>C) ALORS
42 DEBUT_SI
43 AFFICHER "BEUG a le plus d'abonnés en "
44 AFFICHER N
45 AFFICHER "trimestres. Le nombre d'abonnés
est "
46 AFFICHER B
47 FIN_SI
48 SINON
49 DEBUT_SINON
50 AFFICHER "Cé Pa Fèr a le plus d'abonnés en
"
51 AFFICHER N
52 AFFICHER "trimestres. le nombre d'abonnés
est "
53 AFFICHER C
54 FIN_SINON
55 FIN_SINON
56 FIN_ALGORITHME