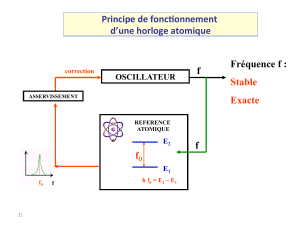
Horloge à réseau optique de mercure neutre : Détermination de la

Horloge `a r´eseau optique de mercure neutre :
D´etermination de la longueur d’onde magique.
Sinda Mejri
To cite this version:
Sinda Mejri. Horloge `a r´eseau optique de mercure neutre : D´etermination de la longueur d’onde
magique.. Physique Atomique [physics.atom-ph]. Universit´e Pierre et Marie Curie - Paris VI,
2012. Fran¸cais. <tel-00806792>
HAL Id: tel-00806792
https://tel.archives-ouvertes.fr/tel-00806792
Submitted on 2 Apr 2013
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

LABORATOIRE DES SYSTÈMES DE RÉFÉRENCE
TEMPS-ESPACE
DU LABORATOIRE NATIONAL DE MÉTROLOGIE ET
D’ESSAIS
THÈSE DE DOCTORAT DE L’UNIVERSITÉ PARIS VI
présentée par
Sinda Mejri
pour obtenir le grade de
Docteur de l’Université Pierre et Marie Curie, Paris VI
Sujet de thèse :
Horloge à réseau optique de mercure : Détermination de la longueur
d’onde magique.
Jury composé de :
Mme. Martina Knoop Rapporteur
M. Gaetano Mileti Rapporteur
M. Ekkehard Peik Examinateur
Mme. Lucile Julien Examinatrice
M. Mourad Telmini Membre Invité
M. Sébastien Bize Membre Invité
M. Philip Tuckey Directeur de thèse

2

Table des matières
1 Etat de l’art des horloges atomiques 9
1.1 Des horloges micro-ondes aux horloges optiques . . . . . . . . . . . . . . 9
1.2 Les horloges à ions piégés . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.1 Performances et limitations des horloges à ions . . . . . . . . . . . 13
1.3 Les horloges à réseau optique . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3.1 Piège dipolaire pour les atomes neutres . . . . . . . . . . . . . . . 14
1.3.2 Solution pour le déplacement lumineux dans une horloge à réseau
optique : longueur d’onde magique . . . . . . . . . . . . . . . . . 14
1.3.3 Réseau optique : confinement dans le régime Lamb-Dicke . . . . . 16
1.3.4 Dynamique des atomes dans le piège . . . . . . . . . . . . . . . . 18
1.3.5 Performances et limitations . . . . . . . . . . . . . . . . . . . . . . 21
1.4 Intèrêts et motivations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.4.1 Motivations et performances envisagées . . . . . . . . . . . . . . . 22
1.5 Conclusion .................................. 27
2 Caractérisation du piège magnéto-optique et mise en évidence du refroidisse-
ment sub-Doppler des isotopes fermioniques du mercure 29
2.1 Refroidissement des atomes de mercure . . . . . . . . . . . . . . . . . . . 30
2.1.1 Refroidissement Doppler . . . . . . . . . . . . . . . . . . . . . . . 30
2.1.2 Refroidissement sub-Doppler . . . . . . . . . . . . . . . . . . . . 31
2.1.3 Structure du niveau 63P1de la raie de résonance 253.7nm . . . . . . 32
2.2 Piège magnéto-optique pour le mercure . . . . . . . . . . . . . . . . . . . 32
2.2.1 Source laser à 253.7nm . . . . . . . . . . . . . . . . . . . . . . . . 33
2.2.2 Description de la chambre à vide . . . . . . . . . . . . . . . . . . . 34
2.2.3 Performance du système à vide . . . . . . . . . . . . . . . . . . . . 35
2.2.4 Technique d’imagerie . . . . . . . . . . . . . . . . . . . . . . . . . 36
2.3 Caractérisation du nuage atomique . . . . . . . . . . . . . . . . . . . . . . 40
2.3.1 Variation du nombre d’atomes en fonction du désaccord de fré-
quence ................................ 40
2.3.2 Evaluation de la température des différents isotopes de mercure . . 41
2.3.3 Dimensions du nuage atomique . . . . . . . . . . . . . . . . . . . 47
2.4 Conclusion .................................. 50
3 Piège dipolaire pour les atomes de mercure 53
3.1 Réalisation d’une source à 724 nm . . . . . . . . . . . . . . . . . . . . . . 54
3.1.1 Mise en place du laser Ti-Saphir . . . . . . . . . . . . . . . . . . . 54
3.1.2 Alignement et tunabilité du Ti-saphir . . . . . . . . . . . . . . . . 56
3.2 Doublage de fréquence . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3

3.2.1 Choix du cristal et application au LBO . . . . . . . . . . . . . . . . 58
3.2.2 Efficacité de conversion . . . . . . . . . . . . . . . . . . . . . . . 60
3.3 La cavité de surtension . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
3.3.1 Principe et choix de la cavité . . . . . . . . . . . . . . . . . . . . . 61
3.3.2 Zone de stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
3.3.3 Compensation de l’astigmatisme . . . . . . . . . . . . . . . . . . . 64
3.3.4 Adaptations de mode . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.3.5 Calcul de l’efficacité de la cavité de surtension . . . . . . . . . . . 66
3.3.6 Adaptation d’impédance . . . . . . . . . . . . . . . . . . . . . . . 66
3.4 Réalisation expérimentale et caractérisation de la source à 362 nm . . . . . 67
3.4.1 Alignement pratique de la cavité . . . . . . . . . . . . . . . . . . . 67
3.4.2 Asservissement de la cavité de doublage . . . . . . . . . . . . . . . 68
3.5 Implementation du piège dipolaire à la longueur d’onde magique . . . . . . 72
3.6 Stabilité du piège dipolaire . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.6.1 Asservissement de la fréquence de la cavité de surtension . . . . . . 76
3.6.2 Asservissement de la puissance . . . . . . . . . . . . . . . . . . . 76
3.6.3 Evaluation de la stabilité du piège . . . . . . . . . . . . . . . . . . 77
3.6.4 Fraction de chargement prévu dans le piège dipolaire . . . . . . . . 78
3.7 Refroidissement des atomes sur une raie étroite . . . . . . . . . . . . . . . 79
3.7.1 Les lasers repompeurs . . . . . . . . . . . . . . . . . . . . . . . . 80
3.7.2 La référence optique pour les diodes lasers . . . . . . . . . . . . . 86
4 Piégeage du mercure et détermination de la longueur d’onde magique 93
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
4.2 Spectroscopie de la transition d’horloge dans le régime de chute libre (rappel) 93
4.2.1 Laser ultra-stable . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
4.2.2 Spectroscopie de la transition horloge . . . . . . . . . . . . . . . . 96
4.3 Piégeage des atomes de mercure dans le réseau optique . . . . . . . . . . . 99
4.3.1 Détection des atomes dans le réseau . . . . . . . . . . . . . . . . . 99
4.3.2 Premières indications du piégeage des atomes de mercure . . . . . 101
4.4 Première mesure de la longueur d’onde magique pour 199Hg........102
4.4.1 Méthode de spectroscopie . . . . . . . . . . . . . . . . . . . . . . 102
4.4.2 Mesure de la fréquence absolue pour deux profondeurs du piège . . 104
4.4.3 Détermination de la longueur d’onde magique à partir de la forme
asymétrique de la raie . . . . . . . . . . . . . . . . . . . . . . . . 106
4.5 Observation des excitations des états de Wannier-Stark . . . . . . . . . . . 107
4