Du côté du site compagnon

Géométrie dans l’espace
Chapitre 13
La ligne de flottaison
Le principe d’Archimède
Eureka! C’est ce que dit Archimède en sortant de sa baignoire.
Il venait de trouver la solution au problème posé par le roi de
Sicile, savoir si sa couronne était en or pur ou non. Pour cela,
il plongea la couronne dans un récipient rempli d’eau à ras
bord, la couronne fit déborder une certaine quantité d’eau
qu’il mesura puis il refit la même expérience avec le même
poids d’or pur. Trouvant des quantités d’eau différentes, il put
ainsi affirmer au roi que sa couronne n’était pas faite d’or pur
démasquant ainsi un joaillier malhonnête!
De là, découle le principe d’Archimède: «Tout corps plongé
dans un fluide reçoit de la part de celui-ci une poussée verti-
cale, dirigée de bas en haut, égale au poids du volume de fluide
déplacé.»
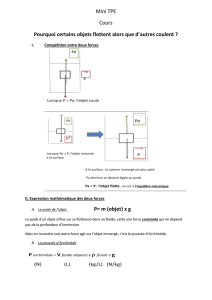
La flottabilité
Le principe d’Archimède permet de définir la flottabilité d’un corps. Elle
dépend du poids réel d’un corps et de la poussée d’Archimède qu’il reçoit
lorsqu’il est plongé dans un liquide.
• Si la poussée d’Archimède est supérieure au poids réel du corps,
celui-ci remonte à la surface: on dit que sa flottabilité est positive.
• Si la poussée d’Archimède est inférieure au poids réel du corps,
celui-ci coule: on dit que sa flottabilité est négative.
• Si la poussée d’Archimède est égale au poids réel du corps, celui-ci
flotte entre deux eaux: on dit que sa flottabilité est nulle.
Or la poussée d’Archimède dépend du volume de l’objet.
Ainsi, un bateau très lourd, construit en métal, peut flotter si son volume génère une poussée d’Archimède qui
compense son poids réel pour obtenir une flottabilité nulle. Mais pourquoi un bateau peut-il flotter alors que sa
maquette, par définition plus légère, ne le peut pas?
Le poids réel d’un bateau est principalement lié à la coque de ce bateau, donc son poids réel est fortement lié à
sa surface. En revanche, la poussée d’Archimède que reçoit un bateau dépend de son volume.
Lorsque l’on fait une maquette d’un bateau, on effectue une réduction de celui-ci en divisant toutes ses dimen-
sions par un même nombre k. Par conséquent, son aire est divisée par k2 mais son volume est divisé par k3.
positive
négative
neutre
Remontée
à l’aide des
gilets

Chapitre 13
Quelques liens utiles
http://www.youtube.com/watch?v=VEdmCMm1SQE
Pour voir une vidéo illustrant la poussée d’Archimède.
http://plongee.amiral.free.fr/formation/niveau4/leprincipedn4.htm
Pour découvrir les applications à la plongée sous-marine de la poussée d’Archimède.
http://cannes.jeunesse.pagesperso-orange.fr/nautism/secret/vcomflot.htm
Pour savoir pourquoi un bateau flotte…
Géométrie dans l’espace
Ainsi, si l’on divise les dimensions d’un bateau par 10, on divise son aire par 100 et son volume par
1 000! Le poids réel de la maquette sera approximativement 100 fois plus petit alors que la poussée
d’Archimède sera, elle, 1000 fois plus petite.
Ainsi, bien que le bateau ait une flottabilité nulle, la maquette, elle, finira au fond des eaux car sa flot-
tabilité est négative.