Partie I : L`UNIVERS

CH 1 : L'Univers connu
I. Structure de l'Univers
I.1 Les ordres de grandeur
Déterminer l'ordre de grandeur d'un nombre c'est indiquer la puissance de 10 la plus proche de ce nombre.
Un ordre de grandeur permet de donner une idée de la valeur d’une grandeur lorsque la valeur exacte ne peut pas être déterminée
ou lorsque cette dernière ne présente pas d'intérêt.
Exemples :
• Diamètre de la Terre : 12 760 km  ordre de grandeur  10 000 km = 104 km
• Prix d'un café : 0,40 €  ordre de grandeur  0,10 € = 10 -1 €
• Vitesse de la lumière : 299 792 km/s  ordre de grandeur  .............................................
Exercice 1 :
VV Cephei A est une étoile de la famille des hypergéantes rouges. Son diamètre est environ 1 100 à 1 900 fois plus important que
celui de notre étoile, le Soleil. Si elle était située à la place de ce dernier dans le système solaire, elle s'étendrait, dans son estimation
haute, jusqu'à l'orbite de Saturne. La luminosité de VV Cephei A est environ 500 000 fois plus forte que celle du Soleil et sa masse
est estimée, selon les techniques de mesure utilisées, entre 30 et 100 M (masses solaires).
a. Déterminer l'ordre de grandeur en km du diamètre de VV Cephei A.
b. Déterminer l'ordre de grandeur de sa masse en masses solaires puis en kg.
c. Pourquoi donne-t-on généralement la masse d'une étoile en masses solaires ?
A noter :
Il existe plusieurs unités pour une même grandeur physique (par exemple le kelvin K ou le degré Celsius °C pour la température).
La conférence générale des poids et mesures établit un système d'unités de référence appelé Système International d'unités (S.I.).
Quelques grandeurs physiques et leur unité S.I. :
Grandeur
Symbole
Unité S.I.
Distance
D, L, H, , ...
Surface
S
Volume
V
Masse
m
Temps, durée
t
Force
F
Pression
P
Intensité électrique
I
Tension électrique
U, V
Puissance
P
Energie
E, Q, W, U, ...
Fréquence
f, N, , ...
Quantité de matière
n
Température
T
Vitesse
v
Données sur le Soleil
• Masse (1 M) : 2,0 10 30 kg
• Diamètre : 1,4 10 6 km
Remarque :
Le symbole d'une unité commence par
une majuscule si l'unité dérive d'un
nom propre, et par une minuscule
dans le cas contraire.
La seule exception à cette règle est le
symbole du litre qui peut s'écrire, au
choix, « l » ou « L », pour éviter les
confusions avec le chiffre 1 ou la lettre
i majuscule (I) selon la police de
caractères utilisée.
1 / 4

I.2 Les structures microscopiques et macroscopiques de l'Univers
Compléter le tableau suivant en s'aidant du diaporama 1.
Ordre de
grandeur
Objet / Structure
Homme
10 0 m
Ordre de
grandeur
Objet / Structure
10 -15 m
10 000 km
10 -10 m
1 000 000 km
10 -5 m
100 000 a.L.
I.3 Que contient principalement l'Univers ?
En 1910, Le physicien anglais Ernest Rutherford
montre expérimentalement que les atomes sont
constitués d'un noyau très petit concentrant la
quasi-totalité de la matière de l'atome. Avant cette
expérience, on pensait que les atomes étaient de
petites sphères pleines de matière.
 E. Rutherford (1871 - 1937)
Exercice 2 :
a. Comparer la taille d'un atome à celle de son noyau.
b. Que trouve-t-on principalement entre les noyaux d'atomes dans le modèle de Rutherford ?
c. Si le noyau d'un atome avait un rayon de 1 mm, quelle serait la taille de l’atome ?
d. Conclure en indiquant de quoi est principalement constituée la matière classique ?
Et à grande échelle ?
La distance moyenne entre les étoiles (distance interstellaire) d'une même galaxie est d'environ 10 16 m. Les étoiles ont un diamètre
allant de 10 6 m (pour les plus petites comme notre Soleil) à 10 9 m pour les plus grandes connues. Entre les étoiles se trouve un vide
appelé vide interstellaire contenant quelques rares atomes, molécules et grains de poussière.
Le vide intergalactique est, quant à lui, beaucoup plus poussé : on y observe moins d'un atome par mètre cube en moyenne.
Exercice 3 :
a. Où trouve-t-on du vide intergalactique ?
b. Que peut-on encore trouver entre les étoiles d'une galaxie ?
c. Si la Terre avait la taille d'un grain de sable, quel serait l'ordre de grandeur du Soleil ? Même question pour les plus grosses
étoiles connues.
d. De quoi est principalement constitué notre Univers ?
A noter :
Le vide est caractérisé par l’absence de particule composant la matière.
Dans le vide parfait, il n’y a donc aucune particule matérielle (atome, électron, nucléon…).
II. Vitesse et distance dans l'Univers
II.1 La vitesse
Exercice 4 :
Un avion parcourt 1850 km en 2,0 h. Combien de kilomètres a-t-il parcourus en 1 h ? En déduire sa vitesse v en km/h
La relation permettant de calculer la vitesse v d'un objet est :
atome plein
Vision de la matière
avant E. Rutherford
noyau plein
vide
Vision de la matière
après E. Rutherford
atome
v : vitesse de l’objet
d : distance parcourue par l’objet
Δt : durée du trajet
2 / 4
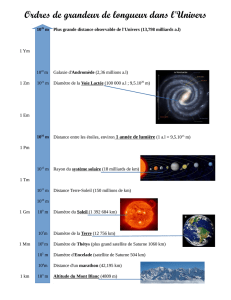
DIAPORAMA 1

II.2 L'année lumière
L'histoire des mesures de la vitesse de la lumière (notée c) ne compte pas
moins d'une douzaine de méthodes différentes. Après les spéculations
d’Empédocle, d’Alhazen ou de Roger Bacon, et les tentatives
malheureuses de Galilée avec des assistants démasquant des lanternes,
la première estimation expérimentale est due à l’astronome danois Ole
Christensen Rømer.
En septembre 1676, il étudie le cycle des éclipses de Io, un satellite de
Jupiter, et remarque que la lumière de Io met 22 minutes de plus pour
nous parvenir sur Terre lorsque la distance entre les deux planètes est la
plus grande (situation B) que lorsqu'elle est la plus petite (situation A). Ce
retard correspond alors au temps supplémentaire nécessaire à la lumière
pour parcourir le diamètre de l’orbite terrestre.
Le problème, c'est qu'à cette époque, le rayon (et donc le diamètre) de
l'orbite terrestre était mal connu. On l'estimait alors entre 70 et 140 millions
de km.
Exercice 5 :
a. Quelle est la relation entre le rayon R d'un cercle et son diamètre D ?
b. En déduire le diamètre moyen de l'orbite terrestre D estimé à l'époque de Rømer.
c. A l'aide du schéma et des données admises à cette époque, déterminer la valeur de la première mesure expérimentale de
la vitesse de la lumière faite par Rømer.
d. Pourquoi Galilée n'avait-il aucune chance de déterminer expérimentalement la vitesse de la lumière avec ses lanternes ?
En réalité la lumière parcourt dans le vide 300 000 km en une seconde.
Ainsi, la vitesse de la lumière (notée c), aussi appelée célérité, vaut : c = 300 000 km/s
Exercice 6 :
Pour mesurer la distance séparant la surface de la Terre et celle de la Lune, on chronomètre la durée nécessaire à un rayon laser
pour faire un aller-retour entre la Terre et un miroir placé à la surface de la Lune.
a. Sachant que le rayon met
t = 2,535 s pour faire l'aller-retour, déterminer la distance d séparant la surface des deux astres.
b. Déterminer la valeur d'une année lumière, distance que parcourt un rayon de lumière en une année.
c. En déduire l'ordre de grandeur d'une année lumière en mètres.
A retenir :
Une année lumière est la distance parcourue par la lumière en une année dans le vide.
II.3 Le temps
La Terre est la troisième planète la plus proche du Soleil. C'est aussi la plus grande
planète tellurique (planète dont la surface est solide) de notre système solaire avec un
rayon d'environ 6400 km. Elle est en moyenne à une distance d = 150 millions de km du
Soleil. De ce fait, comme la vitesse de la lumière n'est pas infinie, l'image du Soleil que
nous observons depuis la Terre est en différée de plus de 8 minutes.
Il nous est donc impossible de voir en direct l'aspect de la photosphère car toute
modification à la surface du Soleil (apparition de tâches solaires par exemple), n'est
visible depuis la Terre que 8 minutes après.
Exercice 7 :
a. D'après ce texte, qu'appelle-t-on photosphère ?
b. Rappeler la valeur de la célérité c de la lumière dans le vide.
c. Rechercher l’expression littérale donnant la durée Δt nécessaire au rayon de lumière pour aller du Soleil à la Terre.
d. Calculer cette durée en secondes puis en minutes. Cette valeur est-elle en accord avec celle donnée dans le texte ?
e. Si le Soleil s’éteignait maintenant, que verrions-nous alors depuis la Terre ?
f. Quelle est la planète la plus proche du Soleil ? Est-elle tellurique ?
g. Donner un exemple de planète non tellurique dans notre système solaire.
Soleil
Terre
Jupiter
et Io
Trajet de la lumière
d'Io vers la Terre
Situation A
Situation B
DIAPORAMA 2
3 / 4

Voir loin, c'est voir tôt !
Ainsi, lorsqu'on regarde le Soleil, on voit une image vieille d'un peu plus de
8 minutes. Autrement dit, on voit le Soleil plus jeune de 8 minutes qu'il ne
l'est en réalité. Pour le dire encore autrement, on voit le Soleil dans le
passé !
Lorsque les astrophysiciens d'aujourd'hui observent par exemple la galaxie
d'Andromède située à 2,5 millions d'années lumières de nous, ils ne
peuvent donc pas voir cette galaxie telle qu'elle est réellement aujourd'hui.
Ils la voient telle qu'elle était il y a 2,5 millions d'années car en une année la
lumière parcourt une distance d'une année lumière.
Exercice 8 :
a. L'image de la Lune que l'on voit depuis la Terre est-elle du direct ?
b. Existe-t-il un moyen de connaître l'état actuel de la galaxie
d'Andromède ou même du Soleil ? Justifer.
c. Comment se nomment les appareils permettant aux astronomes et
aux astrophysiciens d'observer l'Univers à grande distance ?
d. Proxima Centauri est une étoile se trouvant à 4,2 a.L. de la Terre.
Combien de temps met la lumière de cette étoile pour nous
parvenir ?
e. VV Cephei A est l’une des étoiles les plus grandes jamais observée. Elle se situe à 3000 a.L. de la Terre. Si cette étoile
explose aujourd’hui, en quelle année verrons nous cette explosion depuis la Terre ?
f. Exprimer la distance entre VV Cephei A et la Terre en kilomètres. Quel est l’intérêt d’exprimer ce genre de distance en a.L.
plutôt qu’en kilomètres ?
A noter :
• L'année lumière n’est pas l’unité de distance du S.I. mais elle est pratique en Astronomie pour estimer les grandes distances.
• Si les lois de la physique actuellement connues interdisent les "voyages" dans le passé (principe de causalité), il est néanmoins
possible de voir le passé : plus on regarde un objet distant de nous dans l'Univers, plus on remonte le temps.
Conclusion :
Quelle est la réelle motivation des scientifiques qui cherchent continuellement à construire des télescopes de plus en plus puissants
et performants ?
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
...............................................................................................
Exercice 9 : L'unité astronomique
L’unité astronomique (notée u.a.) est égale à la distance séparant la Terre du Soleil, soit 150 millions de km.
a. Sachant que Pluton gravite à environ 5,9 milliards de km du Soleil, exprimer cette distance en u.a.
b. Sachant qu’une année lumière (a.L.) est équivalente à 63 071 u.a., exprimer l’année lumière en km en détaillant les calculs.
c. Betelgeuse de la constellation d’Orion est une étoile 250 fois plus grande que notre Soleil. Elle se trouve à 650 a.L. de la
Terre. A quelle époque fut émise la lumière qui nous parvient de Betelgeuse aujourd’hui ?
DIAPORAMA 3
4 / 4
Télescope spatial Hubble