Application des nombres complexes à l`éléctricité

Application des nombres complexes à l’éléctricité

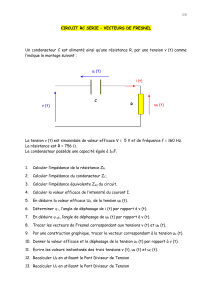
Soit un courant alternatif sinusoïdal dont l’expression en fonction
du temps est :
i = I sin (t + )
I : valeur efficace (en A)
: pulsation (en rad/s)
: phase à l’origine (en rad)
2
x
O
I
A cette grandeur sinusoïdale, nous associons un vecteur
de Fresnel noté .
I

Il en est de même pour la tension u :
Nous pouvons aussi associer à i un nombre complexe :
I
= [ I, ]ou = I (cos + j sin )
I
et
u = U sin (t) = [ U, 0 ]
U
U : valeur efficace (en V)
: pulsation (en rad/s)
Le module correspond à la valeur efficace et l’argument au déphasage.

Exemple :
Un dipôle est parcouru par un courant i = 2 sin (314t + )
quand il est soumis à une tension u = 220 sin (314t ).
2
6
= 314 rad/s
=
6
U = 220 V
I = 2 A
2
Valeurs réelles Valeurs complexes
= [ 220; 0 ] =220(cos 0 + j sin 0) = 220
U
I
= [ 2 , ] = 2 (cos + j sin )
2
6
2
6
6
= 2 ( + j ) = + j
2
3
2
1
2
6
2

Impédance complexe d’un dipôle
Soit un dipôle d’impédance Z, soumis à une tension alternative sinusoïdale
u et parcouru par un courant d’intensité i, on appelle impédance complexe
du dipôle, le nombre complexe :
I
U
Z
où et sont les grandeurs complexes associées à u et i.
U
I