U (ini) - chimphys

m = 50 g
0,29 m/s
Vue de face Vue de droite
poulie
Fils de
connexion
Table
La masse parcourt
1,16 m en 4,0s
m = 50 g
Vue de face Vue de droite
poulie
Fils de
connexion
Table

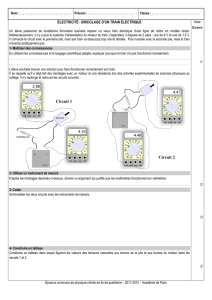
Marine décide de tracer la caractéristique d’une pile alors qu’elle ne dispose pas de résistance réglable.
Pour cela elle a à sa disposition la pile en question, un support d’ampoule sur lequel elle peut visser des ampoules
différentes ( 6V-100 mA , 4V-500 mA, 3,6V-1A ), des fils et des multimètres.
1) Représenter le schéma du circuit, en modélisant les différents
dipôles du circuit décrit ci dessus, puis expliquer comment se servir
de ce montage permettant de réaliser les mesures suivantes : (1)
Aux bornes de la pile précédente, on mesure d’abord la valeur de la tension à vide
E =4,07 V à l’aide d’un voltmètre puis on réalise le montage correspondant au schéma
suivant et on mesure pour chaque ampoule, la tension aux bornes de la pile
(ou de l’ampoule ce qui revient au même ici.
2) Tracer sur une demie feuille de papier millimétrée la caractéristique
de la pile en suivant les consignes suivantes :
l’échelle des intensités traversant la pile variera de 0 à 1A,
celle des tensions aux bornes de la pile variera de 3,0 à 4,2 V (1)
3) Déterminer l’équation de la caractéristique de la pile en précisant
les grandeurs que représente chaque terme ainsi que leurs valeurs et unités. (2)
Aux bornes de la pile, l’équation de la caractéristique est de la forme :
U pile = E –r*I.
Dans cette expression
E représente la tension à vide c’est-à-dire la tension aux bornes de la pile quand elle ne fournit pas de courant,
r sa résistance interne.
E est déterminée en V d’après l’ordonnée à l’origine de la droite
r correspond à la valeur absolue du coefficient directeur de la droite.
(à déterminer sans oublier que l’intensité doit être exprimée en A )
Aux bornes de la pile précédente, on branche seulement en série
un moteur de f.c.é.m. E’ et de résistance interne r’.
4) Représenter le schéma du circuit en modélisant les dipôles. (0,5)
pile 4,5V
U (pile) = -1,10 * I + 4,07
3
3,2
3,4
3,6
3,8
4
4,2
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
U(V)
I(A)
U (moteur)
M
E , r
E’ , r ’
E , r
V
A

Quand on bloque le moteur, l’intensité I b du courant est de 430 mA.
5) Montrer que la valeur de la résistance interne du moteur r’
est voisine de 8 W. Argumenter. (1) La tension aux bornes de la pile est identique à celle aux bornes du moteur :
U pile = U mot soit E - r I = E’ + r’ I . Le moteur étant bloqué, aucun travail mécanique ne peut être transféré par le moteur et
E’ = 0 V d’où r ’ = (E / I) – r = (4,07/ 0,430) –1,1 = 9,4- 1,1 = 8,3 W
Autre méthode , sur la courbe U pile = 3,6 V . Le moteur étant bloqué, il se comporte comme une résistance
r ’ = U pile /I = 3,6 / 0,430 = 8,3 W
6) Expliquez dans ces conditions ce qui peut arriver au moteur si on le maintient bloqué trop longtemps. Argumenter. (1)
Le moteur se comporte comme une résistance , tout le travail électrique qu’il reçoit est transféré sous forme thermique, la
résistance du moteur chauffe énormément, ainsi le moteur peut griller si on empêche rotation
7) Déterminer à partir de la caractéristique précédemment tracée la tension aux bornes de la pile lorsqu’on branche celle-ci sur le
moteur. On fera clairement apparaître le point de fonctionnement sur la courbe. (1)
sur la courbe U pile = 3,8 V .
8) La masse se déplace de 1,16 m en 4,0 s.
a) Déterminer la vitesse de déplacement de la masse. (1)
v = Dz /Dt = 1,16/ 4,0 = 0,29 m/s
b) Donner l’expression de l’énergie cinétique de la masse.
E c = ½ m V2où m représente la masse de valeur constante
déplacée, v la valeur de la vitesse instantanée
(ici correspond ici à une vitesse constante).
Cette énergie varie-t-elle lors de la montée de la masse quand
le moteur fonctionne en régime normal ? (0,5)
L’énergie cinétique reste constante pendant le fonctionnement
du moteur en régime normal)
c) Comment varie l’énergie potentielle de pesanteur de la masse ?
On argumentera à partir de l’expression littérale de cette énergie. (1)
L’énergie potentielle de pesanteur en un point A dépend
du poids de l’objet et
de son altitude z par la relation E pp = mg z (A)
L’altitude augmente alors l’énergie potentielle de la masse aussi
Caractéristique d'une pile 4,5V plate : tension à ses bornes
en fonction de l'intensité qui la traverse
U (pile) = -1,10 * I + 4,07
3
3,2
3,4
3,6
3,8
4
4,2
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
U(V)
I(A)

9) a) Lorsque le moteur fonctionne en régime normal, calculer la puissance relative mise en jeu à chacun des transferts (dont on
précisera le type, l’objet qui fournit le transfert et l’objet qui le récupère) puis les travaux (ou les variations d’énergies
correspondantes) pour un transfert de durée 1,0 s. (4)
Le moteur fonctionnant, les transferts d’énergie sont les suivants pour une durée de 1 s :
Energie interne chimique perdue par la pile : DU = Pchim * Dt = E I * Dt = 4,07*0,250 *1,0 = 1,02 J (0,5)
Travail électrique cédée par effet Joule par la résistance interne de la pile, sous forme de transfert thermique Q à l’air :
W elec ( r ) = P ( r ) * Dt = r I 2* Dt = 1,1*(0,250) 2* 1 = 0,07 J (0,5)
Remarque : le travail électrique total cédé par la pile au moteur est :
W elec ( pile ) = (Pchim -P ( r ) ) * Dt = E I Dt - r I 2 Dt = 0,95 J
Travail électrique cédée par effet Joule par la résistance interne du moteur , sous forme de transfert thermique Q ‘ à l’air:
W elec (r’ ) = P (r’ ) * Dt = r ‘ I 2* Dt = 8,3*(0,250) 2* 1 = 0,52 J (0,5)
Travail mécanique total fourni par le moteur : W méca (tot) = W elec ( pile ) - W elec (r’ )
Travail mécanique fourni par le moteur convertie en énergie mécanique reçue par la masse sous forme d’énergie
potentielle de pesanteur : W m = DEm = DEpp avec DEpp = mgh * Dt = 50*10 -3 *10*0,29* 1 = 0,14 J (0,5)
b) Montrer que la rotation de l’axe du moteur a lieu avec frottement.
On donnera la valeur du travail mécanique correspondant (1)
Travail mécanique perdue par frottement :
W méca (frt) = W méca (tot) - DEpp = (Pchim –P ( r ) - P(r ‘)) * Dt –DEpp = 1,02 –0,07 –0,52 –0,14 = 0,29 J (0,5)
10) Pour une durée de 1,0 s , construire la chaîne énergétique de l’ensemble de la situation pour des transferts (de travail et
d’énergies) entre les systèmes et les convertisseurs qu’on nommera.
Faire figurer chaque valeur des tranferts sur la chaîne. (4) (3) (voir figure)
11) Déterminer le rendement total en énergie acquise par la masse par rapport à celle perdue par la pile. (1)
rdt = DEpp / DU= 0,14 / 1,02 = 0,14 = 14 %

Diagramme de transferts d’énergies pour une durée Dt = 1s
Les valeurs des travaux correspondent à celles des puissances dans ce cas
U(fin)
{ pile}
W F moteur / masse
Par intermédiaire corde
{ masse en interaction avec terre }
U(ini)
Epp (ini)
Résistance
interne r
Moteur
W elec Sortie pile
= E I Dt - r I 2Dt
= 0,95 J
Résistance
interne r ’
Q‘Joule = r’ I 2Dt = 0,52 J
W méca = 0,29 J
frottement
Epp (fin)
{ air }
U(fin) -U(ini) = E I Dt
= 1,02 J
Epp (fin) - Epp(ini)
=mg h Dt = 0,14 J
U(fin) -U(ini) = 1,02 J
U(fin) -U(ini) = 0,88 J
Epp (fin) - Epp(ini) = 0,14 J
Réservoirs d’énergies
Convertisseur { Système }
We(mot)
U(fin)
U(ini)
U(fin) -U(ini)
= 0,88 J