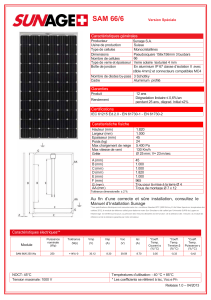
Réactions complexes, en plusieurs étapes:

Réactions complexes, en
plusieurs étapes:
Compatibles avec l’équation de
Michaelis et Menten?

• A l’état stationnaire, par définition:
–d(EA)/dt = 0 = k1[E][A] + k-2 [EAB]-k-1[EA]-k2[EA][B]
–d(EAB-EPQ)/dt = 0 = k2[EA][B]+k-3[EQ][P]-k-2[EAB-EPQ]-k3[EAB-EPQ]
–d(EQ)/dt = 0 = k3[EPQ]+k-4[E][Q]-k-3[EQ][P]-k4[EQ]
–d(E)/dt = 0 = k-1[EA] ]+k4[EQ] -k1[E][A]-k-4[E][Q]
•Loi de conservation des masses:
E + EA + EAB/EPQ + EQ = Etot
• Loi d’action des masses: à l’état stationnaire,
•v = k1[A]∙[E] = k2[EA] = k3[EAB/EPQ] = k4[EQ]
Calcul de la vitesse de réaction à l’état stationnaire:
E  EA  (EAB  EPQ)  EQ  E

Résolution:
•Système de n équations à n inconnues: résolution par le
système des déterminants… Laborieux!
Méthodes « simplifiées »:
La méthode de King et Altman est la plus simple pour le
calcul du dénominateur de l’équation représentant la
vitesse, v = Vmax[ES]/[Etot];
La méthode de Wong et Hanes est plus efficace pour le
calcul du numérateur (aucune simplification de termes
superflus n’est nécessaire).

Dénominateur: King et Altman
Recherche de l’équation,
Analyse « topologique » des
mécanismes d’inhibition par produit