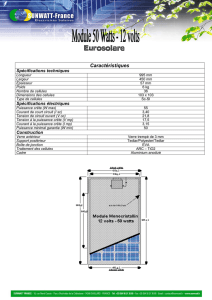
Visualisation de surfaces décrites analytiquement

Visualisation
de surfaces décrites
analytiquement

2
Visualisation de la
fonction y = F(x, z)
PRINCIPE DE BASE
On fixe une coordonnée, par exemple X = Xmax, correspondant à la coordonnée X
la plus proche de l’observateur.
On introduit la notion de crête supérieure et inférieure pour déterminer les parties
visibles à chaque étape;
initialement, ces 2 crêtes correspondent à la section de surface y = F(xmax, z).
x
z
y
X = Xmax -
Y = 0
X = Xmax
Y = 0

3
Visualisation de la
fonction y = F(x, z)
On affiche la section de surface correspondant à X = Xmax.
XXmax.
XXmax -(> 0 fixé)
À l’aide des crêtes supérieure et inférieure courantes, on génère les parties visibles
de la section y = F(X, z); puis, on les affiche.
Mise à jour des crêtes.
Si X Xmin alors réitérez.
Note :
A) Chaque section est décomposée en sous-sections.
Les parties visibles d’une sous-section sont celles au-dessus de la crête
supérieure ou au-dessous de la crête inférieure.
1
3
2

4
Visualisation de la
fonction y = F(x, z)
B) Distinction entre les algorithmes
- mode de représentation des 2 lignes de crête;
- processus de mise à jour des crêtes.
Algorithme de Williamson
1 crête : une suite de segments de droite (ui, vi) -(ui+1, vi+1), i=1, 2, …, N
ui< ui+1
Chaque sous-section d’une section de surface y = F(x, z) est un segment de droite.
Le processus de mise à jour des crêtes et de calcul des parties visibles se ramène à
la comparaison d’une sous-section d’une section de surface avec chaque crête.

5
Comparaison entre le segment
courant et la crête supérieure
Soit (a, b) - (c, d) où a < c, le segment courant,
Déterminer le segment dont les extrémités (uj, vj) et (uj+1, vj+1) sont telles que
uj a < uj+1.
Posons pa = ordonnée du point d’intersection entre la droite verticale u = a
et le segment (uj, vj) -(uj+1, vj+1).
uj < a
pa < b
(a, b)
(a, pa)
(uj, vj)
(uj+1, vj+1)