sujet

Université Pierre et Marie Curie Année Universitaire 2003-2004
Examen de biophysique. Juin 2004
Durée : 2h
Documents et calculatrices interdits. Les téléphones portables doivent être éteints et rangés.
Le sujet comporte deux parties (I. Questions de cours et II. Problème et exercice) qui doivent être rédigées sur deux copies
anonymes différentes (copies avec un coin à rabat). Choisir arbitrairement un numéro d'anonymat (3 chiffres) et l’indiquer
lisiblement sur toutes les copies.
Poser toujours les calculs littéraux avant de passer, s'il y a lieu, à l'application numérique.
I. Questions de cours
1. Décrire avec soin une expérience permettant de mettre en évidence la pression osmotique. On expliquera le rôle joué
par les deux termes, U et TS, dans l'expression du potentiel thermodynamique F = U-TS utilisé pour déterminer la
position d'équilibre.
2. Le sang humain contient 9 g de chlorure de sodium par litre, tandis que l'eau de mer en contient 29 g. Expliquer
pourquoi l'eau de mer n'étanche pas la soif.
3. Pour pouvoir boire pendant la traversée de l'Atlantique à la rame, un rameur exploite le phénomène de l'osmose
inverse pour séparer les ions Na+ et Cl- du solvant (eau douce) en utilisant le dispositif suivant (figure 1) :
Fig.1
Le dispositif est composé d’un cylindre de section S séparé en deux parties par la paroi semi-perméable fixe C (ne
laissant passer que l’eau pure). Les deux extrémités du cylindre sont fermées par les deux pistons mobiles A et B. La
pression extérieure est la pression atmosphérique P0. En exerçant une pression sur le piston situé en A, on force les ions
Na+ et Cl- à rester dans le compartiment AC tandis que de l'eau douce apparaît dans le compartiment BC. On suppose
que la concentration en sel dans le compartiment AC reste constante pendant l’opération.
a. Calculer les concentrations massique c et molaire C du NaCl non dissocié dans l’eau de mer.
b. Calculer, à partir de la loi de Van 't Hoff (donnant la pression osmotique en fonction de la concentration de
soluté), la surpression P1 qu’il faut appliquer pour déplacer doucement le piston A (on suppose que les forces
exercées sur le piston s’équilibrent à tout moment).
c. En déduire le travail W qu'il faut fournir pour produire 3 litres d'eau douce à une température T de 300 K.
d. Combien faudrait-il fournir d'énergie pour récupérer 3 litres d'eau douce prise à 300 K par évaporation ? On
supposera que, à des températures au dessous de 100°C, il faut 4 J pour élever d’1°C la température d’un
gramme d'eau, et que 2200 J sont nécessaires pour vaporiser un gramme d'eau à 100°C. Quelle est la méthode
la plus efficace ?
Données : Masse molaire du NaCl MNaCl = 58 g/mol, masse volumique de l’eau
ρ
e = 1 kg/L, R = 25/3 J K-1 mol-1.
P0+P1 P
0
Eau douce
Eau salée
29 g/L
A B C

II. Problème et exercice
1. Problème
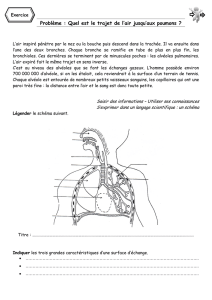
Le problème porte sur le comportement du système respiratoire et du système de circulation sanguine en fonction de
l'altitude (dans l'atmosphère terrestre) ou de la profondeur de plongée.
Données : g = 10 m s-2, R = 25/3 J K-1 mol-1, ln(0,35) ≈ -1, 25/28 ≈ 0,9 ≈ 1/(1,12).
A. Effets de l’altitude.
1. En effectuant le bilan des forces sur une couche d'air d'épaisseur dz en équilibre hydrostatique dans un champ
de gravité g (voir figure 2), établir que
dP(z) = -
ρ (z) g dz,
où
ρ (z) est la masse volumique de l'air.
()
zPF
r
()
dzzP+F
r
volume Sdz d’air, de masse
volumique
ρ (z)
petite surface S
couche élémentaire
d’atmosphère d’épaisseur dz dz
()
zP
()
dzzP +
g
r
champ de gravité
()
zPF
r
()
dzzP+F
r
volume Sdz d’air, de masse
volumique
ρ (z)
petite surface S
couche élémentaire
d’atmosphère d’épaisseur dz dz
()
zP
()
dzzP +
g
r
()
zPF
r
()
dzzP+F
r
volume Sdz d’air, de masse
volumique
ρ (z)
petite surface S
couche élémentaire
d’atmosphère d’épaisseur dz dz
()
zP
()
dzzP +
g
r
champ de gravité
Fig. 2
2. Dans l’atmosphère, la masse volumique
ρ (z) varie en fonction de l’altitude z. Afin de n’étudier que l’effet de
la variation de
ρ , on supposera que la température et l’accélération de la pesanteur sont constantes.
Exprimer
ρ (z) en fonction de la masse molaire M et du volume molaire v(z).
3. Si P0 = 105 Pa est la pression normale au niveau de la mer et que l'atmosphère terrestre obéit à la loi des gaz
parfaits P v = R T, avec : P = P(z) pression totale de l'air à l'altitude z,
v = v(z) = volume molaire,
T = température de l'air = 300 K = constante,
R = constante des gaz parfaits = 25/3 J K-1 mol-1,
réécrire l’équation différentielle obtenue au point 1 en fonction des variables P et z, puis séparer les variables
pour pouvoir intégrer l’équation. L’intégrer pour établir la relation P(z) = P0 exp (- M g z / (R T)).
4. Calculer la constante a = Mg/(RT) pour M= 28 g/mol, T=300 K. Représenter alors P(z) en fonction de z pour
z compris entre 0 m et 30000 m. On aura intérêt à remplir la table suivante :
Table n° 1
z exponentielle P(z)
exp(-1) = 1/2,7 ≈ 0,37
exp(-2) = (1/2,7)2 ≈ 0,14
exp(-3) = (1/2,7)3 ≈ 0,05
5. L'air étant composé de 4 molécules d'azote N2 pour une molécule d'oxygène O2, calculer la pression partielle
PO2(z) en fonction de P(z), puis en fonction de z.
6. Pour que l’hémoglobine du sang puisse se charger en oxygène dans les poumons et le transporter aux tissus, la
pression partielle extérieure de ce gaz, PO2(z), ne doit pas descendre au-dessous de Pmin = 7000 Pa. En déduire
qu'il y a une altitude maximale zmax que l'on ne peut pas franchir si l'on veut continuer à respirer. Calculer cette
altitude et l’indiquer sur le graphe de la question 4.

B. Effets de la pression en plongée sous-marine.
Données : Masse volumique de l’eau
ρ
e = 1 kg/L, g = 10 m s-2.
1. Lorsqu'on plonge dans l'eau, la pression p(h) augmente rapidement en fonction de la profondeur h. En
supposant l'eau incompressible, montrer que la pression augmente d'une atmosphère tous les 10 mètres.
2. Les muscles du diaphragme ne peuvent exercer une force compensant la différence de pression entre
l'extérieur et l'intérieur que si cette surpression est inférieure à 0,1 atm. En déduire la profondeur maximale,
hM, à laquelle on peut encore respirer avec un tuba, c'est-à-dire un tuyau allant de la bouche à la surface.
3. Sachant que le diamètre du tuba est de 2 cm, quel est le volume VT d’air contenu dans un tuba de longueur
égale à la profondeur maximale précédemment trouvée ?
4. L’air rejeté par le plongeur et occupant le volume du tuba n’est pas renouvelé (il reste dans le tuba, empêchant
l’air frais d’y rentrer, et est inspiré à nouveau à la respiration suivante). Si le volume VI inspiré par le plongeur
est de l’ordre de 300 mL, quel pourcentage d’air frais sera contenu dans VI à chaque inspiration ?
5. En faisant l'hypothèse que l'air inspiré doit contenir au moins 70 % d'air frais, quel est l’ordre de grandeur de
la longueur maximale h’M du tuba pour une excursion prolongée et sans fatigue ?
6. Un plongeur décide d'utiliser de l'air pressurisé pour plonger à 100 m de profondeur (plongée avec bouteille)
et équilibrer la pression de l'eau. On suppose donc que la pression de l’air dans les poumons est toujours égale
à la pression hydrostatique extérieure. La loi d'Henry montre que le volume VA d’air dissous dans un volume
VP donné de plasma sanguin est proportionnel à la pression de l'air qui le surmonte, c’est-à-dire à la pression
de l’air contenu dans les poumons. À la pression P0 = 1 atm, on trouve VA /VP = 0,003.
a) Quelle est la proportion VA /VP d'air dissous à 10 mètres de profondeur ? À 100 mètres ?
b) Que se passe-t-il si le plongeur remonte brutalement à la surface ? Décrivez un phénomène
comparable dans la vie courante.
2. Exercice
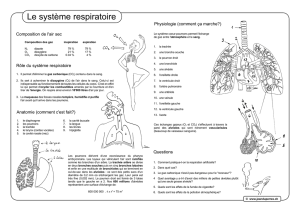
Les alvéoles pulmonaires, situées aux extrémités des bronchioles (alimentées directement par l’air extérieur), peuvent
être assimilées à de petites cavités sphériques, de rayon moyen r = 100 µm, à l’intérieur desquelles la pression est égale
à la pression atmosphérique. L'oxygène de l'air est transmis au sang qui circule dans les vaisseaux par diffusion à
travers la membrane tapissant l'alvéole.
Données : masse volumique de l’eau
ρ
e = 1 kg/L, g = 10 m s-2.
1. En supposant le coefficient de tension de surface égal à celui de l’eau,
σ = 7 ×10-2 J m-2, calculer à partir de la
loi de Laplace la différence de pression
∆ P entre l’intérieur des alvéoles et les tissus pulmonaires
environnants.
2. Sachant qu’un poumon humain contient environ 300 millions d’alvéoles, calculer la surface totale
Σ de contact
entre l’air et la membrane pulmonaire. Comparer cette valeur à la surface qu'offrirait la paroi pulmonaire en
l'absence d'alvéoles. On pourra assimiler grossièrement chaque poumon à un cube de 20 cm de coté.
3. Lors d’une inspiration, les muscles du thorax et du diaphragme, qui accroissent la surface d’échange air-
liquide de 10 m2 en dilatant les alvéoles, luttent contre la tension superficielle des parois alvéolaires. Calculer
le travail W à fournir lors d’une inspiration pour gonfler les alvéoles, en l’exprimant en fonction de la variation
d’énergie libre correspondante.
4. Faisons l’analogie avec un individu allongé qui soulève d'une hauteur h = 1 cm une masse m posée sur sa
poitrine. Pour quelle valeur de m («masse équivalente») le travail fourni par cet individu est-il égal au travail
W calculé à la question 3 ?
5. En réalité, les cellules de la membrane alvéolaire synthétisent un « surfactant », c’est-à-dire des molécules
tensioactives qui abaissent la tension superficielle en se concentrant à l’interface air–liquide. Ce mélange de
phospholipides divise par environ 3 la tension superficielle du liquide. Dans ces conditions, que devient le
travail W à fournir, et la «masse équivalente» m à soulever ?
6. Sachant que la quantité de surfactant à l’intérieur de chaque alvéole reste constante durant la respiration,
expliquer qualitativement pourquoi la tension superficielle du film alvéolaire varie durant la respiration, et
comment cette variation permet de maintenir l’équilibre de pression entre l’alvéole et l’extérieur au cours du
cycle respiratoire.