[fi 12: 270

GEOMETRIE. ipg
mente de deux droits, est plus grand que lu somme des deux
(iiilres angles ( 190 ).
Lorsqu'un triangle spherique contient un angle droit, il est
rectangle: son hypoténuse est le cùté opposé à l'angle droit. Un
triangle spherique qui contient deux ou trois angles droits, est
appelé bi-reclangle ou tri-rectangle (187). Trois grands cercles
perpendiculaires deux à deux divisent évidemment la surface
spherique en huit triangles tri-rectangles égaux entre eux. Ainsi,
le triangle tri-rectangle est le huitième de la surface spherique.
III. — Mesure de la surface spherique.
270. On appelle ligne brisée régulière une ligne brisée
plane et convexe, dont les côtés forment des angles égaux et
sont égaux.
Lne ligne brisée régulière jouit de toutes les propriétés d'un
polygone régulier : elle est inscriptible et circonscriptible au
cercle, elle a un centre, un rayon, un apothème. Seulement,
l'angle au centre d'une ligne brisée régulière n'est pas, en gé-
néral, une partie aliquote de quatre angles droits. On appelle
diamètre d'une, ligne brisée régulière toute droite passant par
son centre.
Pour inscrire une ligne brisée régulière dans un arc de
cercle, il suffit de diviser cet arc en parties égales et de joindre
les points de division par des cordes.
271. La surface engendrée par une ligne brisée régulière en
tournant autour d'un diamètre qui ne la traverse pas, a pour
mesure le produit de la circonférence
'"' ~' ' inscrite dans la ligne brisée par la
projection de cette ligne sur l'axe
[fi
12: 270
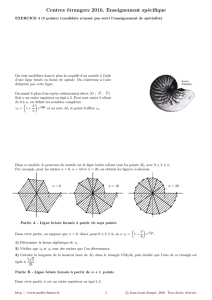
Soient 0 le centre et 01 l'apothème
delà ligne brisée régulière ABCD tour-
nant autour du diamètre xy. La sur-
\ i ; ; ! ! ! ! i face engendrée par cette ligne sera la
'*. i; ! ! ! somme des surfaces engendrées par les
X4L___A;/ côtés
AB, BC, Cl).
Le côté AB engendrera la surface
convexe d'un cône ayant AE pour hauteur et BE pour rayon
de sa base. L'expression de celte surface est égale à la hauteur
\E multipliée par la circonférence, ayant pour ra\on la per-
pendiculaire élevée sur le milieu du côté jusqu'à la rencontre
de l'axe (23V) : cette perpendiculaire est précisément l'apo-
thème 01 de la ligne brisée régulière. On pourra donc écrire
surf AB = AE.circ01.