Leon 2 - loirecambodge

Chapitre 3 Oscillations Leçon 2 Circuit RC
Leçon 2 . LE CIRCUIT RC
Rappels
- Les conventions en électricité
On choisit un sens positif du courant (flèche de i) et on lui associe la tension aux
bornes du dipôle D (flèche de u).
Deux choix de convention sont possibles :
convention récepteur : les deux flèches sont de sens
opposé
convention générateur : les deux flèches sont de même
sens
D
u
i
D
u
i
- Les notations en électricité
Les majuscules représentent des grandeurs constantes comme Q, U, I
Les minuscules représentent des grandeurs instantanées, grandeurs variant au cours du
temps, comme q, u, i
- Conseils pour résoudre un problème d'électricité
représenter le circuit
choisir le sens de l'intensité représentée par une flèche sur le conducteur
flécher les tensions en les accompagnant d'un symbole
Exercice 1 : charge d'un condensateur à courant constant
Un condensateur de capacité C est chargé par un générateur de courant. L'intensité I du
courant est constante et égale à 0,14 mA. Quand la charge commence, la tension UAB aux
bornes du condensateur est nulle. Après une durée de charge T = 10 s, UAB = 0,64 V.
Calculer C
B
+ -
+ -
AUAB
Q -Q
Relation entre la capacité C du condensateur et la charge : AB
A
U
Q
C=
QA = I T ABU
IT
C= C = 64,0
1010.14,0 3
×
− C = 2,2.10-3 F
Pour décharger le condensateur, il suffit de déconnecter le générateur et de relier les
armatures du condensateur par un fil conducteur. Alors UAB→0
Pendant la charge, le condensateur se comporte comme un récepteur ; pendant la
décharge, il se comporte comme un générateur.
62

Chapitre 3 Oscillations Leçon 2 Circuit RC
Exercice 2 : où est passée l'énergie ?
Un condensateur de capacité C = 10 µF est chargé sous une tension U = 50 V. Il est
déconnecté du circuit de charge puis ses armatures sont reliées à celles d'un condensateur
de capacité C' = 2C initialement déchargé et isolé.
Les condensateurs prennent alors des charges Q1 et Q'1 sous une même tension U'.
1. Exprimer Q1 et Q'1 en fonction de U'.
2. En déduire U' en fonction de U, C et C'.
3. Calculer U', Q1 et Q'1.
4. Quelle est l'énergie initiale du condensateur de capacité C ? Quelle est l'énergie finale
de l'ensemble ? Commenter.
________________________
+ -
+ -
U
Q -Q
Condensateur en fin de charge, une fois déconnecté :
Q = CU
Association des 2 condensateurs :
L'état d'équilibre est atteint, l'intensité dans les fils
de connexion est nulle.
1. Q1 = CU' et Q'1 = C'U'
2. Au cours de l'association, le condensateur de
capacité C se décharge partiellement dans le
condensateur de capacité C' sans perte de charge : Q = Q1 + Q'1
CU = CU' + C'U' = U'(C+C') U
'CCC
'U + =
+ -
+ -
U'
Q'1 -Q'1
+ -
+ -
Q1 -Q1
3. C' = 2C U
C3
C
'U = 3
U
'U = U' = 3
50 U' = 17 V
Q1 = CU' 3
CU
Q1= 3
5010.10
Q6
1
×
=− Q1 = 1,7.10-4 C
Q'1 = C'U' = 2CU' = 2Q1 Q'1 = 3,3.10-4 C
4. Energie initiale du condensateur de capacité C : E1
E1 = 2
1CU2 E
1 = 2
1×10.10-6×502 E1 = 1,3.10-2J
Energie finale de l'ensemble : E2
E2 = 2
1CU'2 + 2 1C'U'2 E
2 = 2
1(C+C')U'2
U' = 3
U E
2 = 2
1(3C)
()
2
3
U E
2 = 2
13
CU2 3
E
E1
2= E2 = 4,2.10-3 J
La perte d'énergie provient de la dissipation par effet Joule dans les fils de jonction,
lors de la réunion des 2 condensateurs.
63

Chapitre 3 Oscillations Leçon 2 Circuit RC
Exercice 3 : Charge d’un condensateur
Pour charger un condensateur de capacité C = 1 µF, on réalise un circuit série orienté dans
le sens indiqué sur la figure ci-dessous et comprenant :
C
A
N
P
B
K
i
R
- un générateur, de résistance interne nulle, délivrant une tension constante UPN = E ;
- un conducteur ohmique de résistance R ;
- le condensateur initialement déchargé ;
- un interrupteur K .
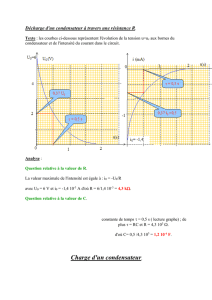
A l'instant choisi comme origine des temps (t = 0), on ferme K. Les variations de la charge
q = qA de l'armature A du condensateur sont données par la courbe suivante (la tangente à
cette courbe à l'instant t = 0 a également été tracée).
1. Vers quelle valeur tend uAB quand t →
∞
? En déduire, en s'aidant de la courbe, la
valeur numérique de E.
2. Montrer que l'intensité i0 du courant à la date t = 0 (début de la charge) vaut i0 = R
E.
3. a) Pourquoi peut-on affirmer que l'intensité du courant dans le circuit, à un instant de
date t quelconque, est donnée par le coefficient directeur de la tangente au point de la
courbe d'abscisse t ?
b) En utilisant la remarque du a) :
déterminer la valeur numérique de i0. En déduire la valeur numérique de R.
justifier, en s'aidant du graphique, l'évolution de i en fonction du temps.
4. Déterminer, à partir de la courbe, les valeurs numériques de uAB, uPN et i, à l'instant de
date t = 10-2 s. En déduire l'énergie stockée dans le condensateur à cet instant.
64

Chapitre 3 Oscillations Leçon 2 Circuit RC
1. Pour t →∞, le condensateur est chargé. Le
courant ne passe plus : uR = 0 ;
uAB = uPN = E
Sur la courbe on lit qA = 10-5 C
u
K
A
N
P
B
uAB
uPN
i
uR
AB = C
qA E =
C
qA qA en C, C en F,
E
E =
en V
6
5
10
10−
−E = 10 V
2. A t = 0 , le condensateur n'est pas
chargé : uAB = 0
donc uPN = E = Ri0 i
0 = R
E E en V, R en Ω, i0 en A
3. a) A une date t quelconque, on peut écrire la relation charge-intensité : dt
dq
i
A
=
mathématiquement i est la dérivée de qA = f(t). Elle est donnée par le coefficient directeur
de la tangente à la courbe au point d'abscisse t
b) A t = 0 i = i0
0
A
0dt
dq
i⎟
⎠
⎞
⎜
⎝
⎛
=
point M de la tangente de coordonnées t = 10-2 s, qA = 10-5 C
i0 = 0M
0M
tt
qq
−
− i
0 = 2
5
10 i
10
−
−
0 = 1.10-3 A i0 = 1 mA
i0 = R
E R =
0i
E R = 3
10
10
− R = 104 Ω R = 10 kΩ
Quand t augmente le coefficient directeur de la tangente à la courbe qA = f(t) décroît, donc
i décroît. Pour t →∞, i → 0
5. A la date t = 10-2 s, point P de la courbe qA = f(t), on lit qA = 6.10-6 C
uAB = C
qA u
AB = 6
6
10
10.6
−
− uAB = 6 V
uPN = E uPN = 10 V
4
ABABPN
R10 610
i
R
uE
i
R
uu
i
R
u
i−
=
−
=
−
== i = 4.10-4 A
Energie stockée dans le condensateur à cette date : E = 2
1C.uAB2 C en F, uAB en V,
E en J E = 2
1×10-6×(6)2 E = 1,8.10-5 J
65

Chapitre 3 Oscillations Leçon 2 Circuit RC
Exercice 4 : étude de la décharge d'un condensateur
Le montage ci-contre permet
d'étudier l'évolution de la
tension aux bornes d'un
condensateur de capacité C en
série avec une résistance R.
Le commutateur (interrupteur à
p
lusieurs positions) a deux
p
ositions possibles repérées
p
ar 1 et 2. Une interface, reliée
à un ordinateur, permet de
saisir les valeurs instantanées
de cette tension uC.
D
onnée: E=5,0V.
i
B
2 R A
C
E
1 uR
uc
Initialement, le commutateur est depuis longtemps en position 2 et le condensateur est déchargé.
I Dès lors, comment faut-il manipuler le commutateur pour obtenir la courbe du document 1 ci-
dessous donnant l’évolution de la tension uC aux bornes du condensateur en fonction du temps ?
0
1
2
3
4
5
6
0 0 0,04 0,06 0,08 0,12 0 0,16,02 0,1 ,14
0 20 100 140 t en m
s
UC en
volts
Document 1
1. En respectant les conventions d’orientation du schéma du circuit:
a) préciser le signe de l’intensité i du courant de décharge.
b) Écrire la relation entre l’intensité i du courant et la tension uR
c) Écrire la relation entre la charge q de l’armature A du condensateur et la
tension uC
d) Écrire la relation entre l’intensité i et la charge q
e) Écrire la relation entre les tensions uR et uC lors de la décharge
66