Amphi 8_25.03.2015 Fichier

Physique statistique (PHY433)
Amphi 8
Thermodynamique du rayonnement
Thermodynamique
du
rayonnement
,
gaz de photons
Gilles Montambaux
Planck (1900)
11
«
Planck
» (2013)
25 mars 2014
Planck (1900)
«
Planck
» (2013)
Le contrôle…
Le contrôle aura lieu le mardi 31 mars de 9h à 12 h
Aucun document autorisé.
Tablette ordinateur et téléphone strictement interdits
Tablette
,
ordinateur
et
téléphone
strictement
interdits
.
Calculatrice recommandée.
Un formulaire sera distribué.
2
Thermodynamique du rayonnement électromagnétique
Rayonnement et transferts d’énergie
ex: équilibre thermique de la terre
rayonnement cosmologique
Lasers
rayonnement
cosmologique
Lasers
S
p
ectre du cor
p
s noir Effet
p
hotoélectri
q
ue
pp
Planck 1900
pq
Einstein 1905
Débuts de la révolution quantique 19211918
Thermodynamique du rayonnement
gaz de photons
gaz
de
photons
Plan du cours
I. Densité d’énergie du rayonnement électromagnétique
Loi de Planc
k
« spectre du corps noir »
II. Equilibre soleil-terre, constante solaire, effet de serre
III. Aux origines de la mécanique quantique
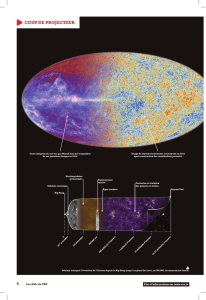
IV Rayonnement fossile de l’univers
IV
.
Rayonnement
fossile
de
l’univers
4

Thermodynamique du rayonnement électromagnétique
Quelle est la distribution d’équilibre du champ électromagnétique
dans une « boîte » à la température T ?
corps noir
ité i b b f it t l t
«
corps
noir
» :cav
ité
qu
i
a
b
sor
b
e par
f
a
it
emen
t
l
e rayonnemen
t
et le réémet en équilibre à la température T
Kirchhoff (1859)
T
T
Thermodynamique du rayonnement électromagnétique
Quelle est la distribution d’équilibre du champ électromagnétique
dans une « boîte » à la température T ?
corps noir
ité i b b f it t l t
«
corps
noir
» :cav
ité
qu
i
a
b
sor
b
e par
f
a
it
emen
t
l
e rayonnemen
t
et le réémet en équilibre à la température T
Kirchhoff (1859)
La densité d’énergie
est une fonction universelle qui ne dépend
que de la fréquence et de la température
T
que
de
la
fréquence
et
de
la
température
T
expérience
Wien (1893
)
Wien
(1893
)
Thermodynamique du rayonnement électromagnétique
Quelle est la distribution d’équilibre du champ électromagnétique
dans une « boîte » à la température T ?
corps noir
ité i b b f it t l t
«
corps
noir
» :cav
ité
qu
i
a
b
sor
b
e par
f
a
it
emen
t
l
e rayonnemen
t
et le réémet en équilibre à la température T
Kirchhoff (1859)
Un des deux grands problèmes
T
Un
des
deux
grands
problèmes
de la physique classique fin XIXème
T
Planck 1900
Ei t i
1905
Ei
ns
t
e
i
n
1905
Spectre du corps noir
T
Densité d’énergie par unité de volume et de fréquence à la température
T
contient deux « ingrédients » distincts
Énergie moyenne d
’
un mode de fréquence à la température
Énergie
moyenne
dun
mode
de
fréquence
,
à
la
température
Ditéd dd tàlfé
D
ens
ité
d
e mo
d
es
d
u rayonnemen
t
à
l
a
f
r
é
quence
8

Modes du rayonnement électromagnétique dans une cavité
Champ électromagnétique : solution de
« Mode propre »
avec
Un «
mode propre
»d
’
oscillation du champ dans une boîte est caractérisé par
Un
«
mode
propre
»
d oscillation
du
champ
dans
une
boîte
est
caractérisé
par
son vecteur d’onde
sa fréquence
Énergie moyenne d’un mode de fréquence , à la température
Le potentiel vecteur obéit à l’équation d’onde
Energie associée à un mode
avec
Chaque mode propre est un oscillateur harmonique de pulsation
Quantification de l’oscillateur harmonique 10
É
Rappel : quantification de l’oscillateur harmonique
É
nergie d’un mode propre d’oscillation
Énergies propres
Formalisme canonique
Rappel : énergie moyenne de l’oscillateur harmonique à température T
cf. amphi 3, p.16
Formalisme
canonique
11
Rappel : quantification de l’oscillateur harmonique
Etat d’excitation moyen de l’oscillateur
à la température T
classique
Identique au facteur de Bose
pour un gaz de particules d’énergie
en contact avec un réservoir à
photons 12

Chaque mode propre du champ électromagnétique
est un oscillateur harmonique de pulsation
U h t d’é i
= Etat d’excitation de l’oscillateur
U
n p
h
o
t
on ,
d’é
nerg
i
e
est un degré d’excitation de l’oscillateur harmonique
= Nombre de photons dans le mode
est l’état moyen d’un oscillateur
d’énergie à température T
C’est aussi le nombre moyen de photons d’énergie à température T
Énergie moyenne d’un mode e.m.
M oscillateurs harmoniques
Planck (1900) , Einstein Bose (1924)
bosons en nombre indéterminé
dans M états quantiques
dans
M
états
quantiques
X
X
X
X
Microétat
= ensemble des degrés
d
’
excitation des oscillateurs
Microétat
= nombre de photons
dans un chaque état quantique
d excitation
des
oscillateurs
Formalisme canonique Formalisme grand-canonique
cf.amphi 5, p. 50
Degré d’excitation moyen d’un oscillateur
de pulsation Nombre moyen de photons d’énergie
en nombre indéterminé
Spectre du corps noir
T
Densité d’énergie par unité de volume et de fréquence à la température
T
contient deux « ingrédients » distincts
Énergie moyenne d
’
un mode de fréquence à la température
Énergie
moyenne
dun
mode
de
fréquence
,
à
la
température
Ditéd dd tàlfé
D
ens
ité
d
e mo
d
es
d
u rayonnemen
t
à
l
a
f
r
é
quence
15
Densité de modes du rayonnement à la fréquence cf. amphi 6, p.13-17
= nombre de modes dans une tranche de fréquence D(ν)dν
On définit aussi
dν
[
ν,ν+dν
]
= nombre de modes de fréquence inférieure à
N
<
(ν)
d
N
(
ν
)
ν
N
(
)
X
Θ
(
)
ν
D(ν)=
d
N
<
(
ν
)
dν
N
<
(
ν
)
=
X
k
Θ
(
ν−ν
k
)
( s’appelle aussi densité intégrée )
N
<
(ν)
Dans la limite du continuum
,
N
<
(
ν
)
=
µ
L
¶
3
Z
d
3~
k
car dans une boîte de taille , les valeurs de sont multiples de
L
~
k
2π
L
,
N
<
(
ν
)
µ
2π
¶
Z
ν(~ k)<ν
d
k
L
N
<
(
ν
)
=VVolume de l’espace des ~
k|ν
~
k
<ν
(
2
)
3
<
(
)
(
2
π
)
3
16

Densité de modes du rayonnement à la fréquence cf. amphi 6, p.13-17
N
<
(ν)=2VVolume de l’espace des ~
k|ν
~
k
<ν
(
2
π
)
3
( x 2 polarisations)
(
2
π
)
3
8
π
ν
3
V
4
π
k
3
=
8
π
3V
ν
3
c
3
N
<
(ν)=2
V
(2π)
3
4
π
k
3
cf. amphi 6, p.14
D(ν)∝νd−1
D
(
ν
)
=V8π
3
ν2
D
(
ν
)
=dN
<(ν)
d
(
)
c
3
(
)
d
ν
Densité de modes électromagnétiques dans une cavité de volume V,
(physique classique) Rayleigh (1900) 17
Spectre du corps noir
T
Densité d’énergie par unité de volume et de fréquence à la température
T
Énergie moyenne d’un mode
Densité de modes
D
(
ν
)
=V8π
3
ν
2
(
)
c
3
Loi de Planck
rayonnement
du corps noir
u(ν,T)= 1
VD(ν)kT =8π c3ν2kT
hν¿kT
Rayleigh-classique densité de modes x énergie moyenne / mode
(équipartition de l’énergie)
Planck
Wien
Loi de Planck
est une fonction universelle
Loi du déplacement de Wien
Loi de Planck