TESLA, OUI… (CONSIGNES)

Comprendre
10 T
ESLA, OUI… (CONSIGNES)
1. Champ magnétique
1.1. Découverte du magnétisme
I.1.1. En l'absence de tout objet, l''environnement autour de l'aimant semble-t-il modifié ?
Rien d'apparent n'est modifié.
I.1.2. Quels objets sont "sensibles" à l’action de l’aimant ?
Les objets contenant du fer.
I.1.3. L’action de l’aimant nécessite-t-elle le contact entre celui-ci et l’objet ? Que peut-on en déduire ?
Un contact n'est pas nécessaire. L'aimant agit à distance.
I.1.4. De quel matériau étaient vraisemblablement constitués les clous des sabots des bergers mentionnés par Thalès ?
Les clous contenaient du fer.
I.1.5. En dehors de tout matériau magnétique ou ferreux, quelle caractéristique de notre environnement la boussole met-elle en
évidence ?
La boussole indique la direction du champ magnétique terrestre.
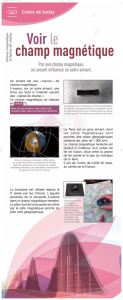
I.1.6. Que remarque-t-on lorsqu'on déplace la boussole autour de l'aimant ?
La boussole prend une direction privilégiée. Elle pointe vers l'extrémité de l'aimant.
I.1.7. Que crée l'aimant dans son environnement proche ?
Un aimant crée un champ magnétique.
1.2. Spectre magnétique
I.2.1. Quel nom donne-t-on aux lignes tracées ?
Ce sont des lignes de champ
I.2.2. Quel est l'orientation (sens) de ces lignes par rapport à l'aimant ?
Les lignes de champ sont orientées dans le sens pris par l'aiguille aimantée, du nord
vers le sud de l'aimant.
1.3. Caractéristiques du champ magnétique
point A B C D A’ B’
B
x
(mT)
1.3.1. Aux incertitudes de mesures près, que peut-on dire de Bx(A) et Bx(A'),de Bx(B) et Bx(B').
Bx(A) = – Bx(A'), Bx(B) = – Bx(B'
1.3.2. En déduire les valeurs de Bx(C'), Bx(D'). Comment peut-on interpréter l’existence de valeurs négatives ?
Bx(C') = – Bx(C), Bx(D') = – Bx(D)
1.3.3. Comment peut-on interpréter l’existence de valeurs négatives ?
Le signe négatif indique que le champ magnétique a changé de sens par rapport à la
sonde.
1.3.4. Aux incertitudes de mesures près, que peut-on dire de Bx(C) et Bx(D). Que peut-on en déduire ?
Bx(B) = Bx(C) : il existe une symétrie par rapport à l'axe de l'aimant.
1.3.5. Comparer Bx(A) et Bx(B). Que peut-on en déduire ?
Bx(A) > Bx(D) : la valeur de Bx diminue avec la distance à l’aimant.
1.3.6. Le champ magnétique est-il un champ scalaire ou un champ vectoriel ? Argumenter.
Au champ magnétique on peut associer une valeur mais aussi un sens (signe –) et une
direction (celle de l’aiguille aimantée), il s’agit donc d’un champ vectoriel.
1.3.7. Argumentation sur la comparaison.
On vérifie que le vecteur champ magnétique est
tangent aux lignes de champ en chaque point, que
le spectre présente une symétrie axiale, que la
valeur de B (proportionnelle à la longueur du
vecteur) diminue avec la distance à l’aimant et/ou
que les lignes de champ se resserre aux pôles.
2. Champ électrostatique
2.1. Déviation d'un faisceau d'électron
2.1.1. Quand les plaques horizontales ne sont pas alimentées, quelle est la trajectoire des électrons ?
La trajectoire est une droite horizontale
2.1.2. Quand les plaques horizontales sont alimentées (première partie de l’expérience), que devient la trajectoire des
électrons ? Cela était-il prévisible ? Argumenter.
C’est un arc de parabole vers le bas
C’était prévisible car les électrons chargés négativement sont attirés par la plaque
positive.
2.1.3. En faisant le parallèle avec le mouvement des projectiles dans le champ de pesanteur, déterminer la direction et le sens
du champ électrostatique existant entre les deux plaques horizontales
Le vecteur champ électrique est vertical.
2.1.4. Qu’en est-il lors de la deuxième partie de l’expérience ?
Le vecteur champ électrique est toujours vertical mais il a changé de sens.
2.1.5. De quoi dépend le sens du vecteur champ électrostatique ?
Il dépend du signe des plaques
2.2. Lignes de champ dans un condensateur plan
2.2.1. Les petits grains se disposant parallèlement aux lignes de champs, dessiner ci-contre l’allure
de celles-ci.
2.2.2. Par rapport aux deux "plaques", quelle est la direction d'une ligne de champ ?
Les lignes de champ sont perpendiculaires aux plaques.
2.2.3. Cela est-il en accord avec les observations du paragraphe 2.1. ?
Oui, le vecteur champ électrique était perpendiculaire aux plaques (plaques
horizontales, champ vertical)
2.2.4. Le champ obtenu est-il un champ uniforme ? Argumenter.
Les lignes de champ sont parallèles entre elles et régulièrement espacées, le champ est
donc uniforme.
2.3. Mesure de la valeur E du champ électrostatique
2.3.1. Que peut-on dire de la valeur de U lors d'un déplacement parallèle aux électrodes ?
La valeur de U reste approximativement constante.
2.3.2. On utilise parfois le terme de lignes équipotentielles ? Quelle est leur direction par rapport aux lignes de champ ?
Une ligne équipotentielles est une ligne sur laquelle la valeur de U est constante.
Ces lignes sont perpendiculaires aux lignes de champ.
2.3.3. Relever les valeurs de la tension U en suivant une ligne de champ pour quelques valeurs de la distance d entre la sonde
et l'électrode négative. Calculer le rapport U/d avec d en mètre.
d (cm) 4,0 6,0 8,0 10,0
U (V)
4,0 6,0 8,0 10,0
U/d (V.m
–
1
)
1,0×10
2
1,0×10
2
1,0×10
2
1,0×10
2
2.3.4. Aux incertitudes de mesures près, que constate-t-on pour les valeurs de U/d ?
On constate que le rapport U/d est constant.
2.3.4. Choisir(entourer) dans les tracés suivants celui qui traduirait les variations de U en fonction de d :
2.3.5. Cela conforte-t-il la réponse à la question 2.2.4 ?
Oui car à l’intérieur d’un condensateur plan, le champ est uniforme