Introduction à la Physique des Particules Fondamentales

1
Introduction à la Physique des Particules
Fondamentales
Professeur : Allan G. Clark
Assistant : Andrew Hamilton, Alexander Korzenev
Bibliographie
1. * Introduction to High Energy Physics (4ième édition), D. Perkins (Cambridge)
2.* Introduction to Elementary Particles (2ième édition), D. Griffith (Wiley)
4. The Physics of Particle Detectors, O. Green (Cambridge)
5. Quarks and leptons, F. Halzen and A. Martin (Wiley)
6. Particle Astrophysics, D. Perkins (Oxford)
Le but de notre cours
Le but de notre cours est d'étudier les propriétés des particules élémentaires et les
interactions entre les particules.
Préparation pour le Cours
Chapitre 1 de D. Griffith : Introduction to Elementary Particles
Autres cours
Introduction à la Physique des Noyaux X. Wu
Particules dans l’Univers D. Rapin
Physique des Détecteurs D. Rapin
Mécanique Quantique II M. Maggiore
Semestre d'été, 2011

2
Introduction à la Physique des Particules
Fondamentales
Université de Genève
Semestre d’été 2011
Professeur : Allan G. Clark
Assistant : Andrew Hamilton, Alexander Korzenev
Chapitre 1
Introduction – Les Particules Fondamentales et leurs Interactions
Bibliographie: Griffiths Chapitre 1
La théorie de la physique des interactions entre les particules fondamentales (ou
élémentaires) est un exemple spectaculaire de la théorie des champs, et les effets des
lois d’invariance sur cette théorie. Même si les calculs seront parfois difficiles, les idées
à la base de la théorie sont très simples :
- Il y a un nombre limité des particules, identifiées par leur masse et les nombres
quantiques internes ;
- Il y a un nombre limité des forces qui agissent entre les particules ;
- Les forces et la matière évoluent en espace-temps, et le vide est un composant
actif dans les interactions.
La théorie a été établie à partir d’expériences, qui ont progressivement élargi les limites
de validité de la théorie. Ces limites continueront à étendre, avec la construction des
nouveaux accélérateurs, et avec le développement de l’instrumentation pour les
détecteurs sophistiqués.
1.1 Les particules fondamentales, selon notre connaissance actuelle
a) Selon notre définition, les particules fondamentales sont des particules ayant
aucune structure spatiale connue, qu’on dit ’ponctuel’ ou ‘point-like’. Ils sont de
2 types : les bosons et les fermions.
b) Les fermions sont les particules de la matière. Ils sont ponctuels, avec un
moment angulaire intrinsèque, qu’on appelle spin, de
€
J=1 2
, et ils obéissent la
statistique de Fermi. Il y a deux catégories : les leptons et les quarks. Pour
chaque fermion, il existe un anti-fermion, ayant la même masse mais avec les
nombres quantiques internes (sauf peut-être les neutrinos) opposées. Les
fermions et les anti-fermions peuvent s’annihiler en énergie, ou se créer en paire
avec suffisamment d’énergie.

3
c) Les interactions correspondent à l’échange des bosons de jauge, et ils ont un
moment angulaire J=1 (vectoriel). Ils obéissent la statistique de Bose.
d) Certaines théories (supersymétrie) associent pour chaque particule de J=1/2, un
partenaire ayant J intégral, et vice-versa. A ce jour, aucune particule super-
symétrique a été découverte.
1.1.1 Les leptons, les quarks et leurs saveurs (flavor)
a) Les 6 leptons se répartissent en 3 doublets (familles ou saveurs) selon notre
connaissance expérimentale, avec charge électrique Q=0 ou Q=-1. Les
masses sont de 0.511 MeV (e-), 105 MeV (µ−) et 1.78 GeV (τ−). Les masses
des neutrinos sont inconnues, et très faibles.
€
Q=0 ν
e
νµ ντ < 3 eV < .19 MeV < 18 MeV
Q=−1 e- µ
-
τ
- .51 MeV 105 MeV 1.78 GeV
Le 1 0 0
L
µ
0 1 0
L
τ
0 0 1
L’absence des désintégrations
€
µ
−→e−
γ
indique une loi de conservation dans
les désintégrations. Egalement l’existence de 3 types de neutrino est
démontrée, aussi bien que la conservation de saveur leptonique (presque – il y
a des oscillations entre les différents types de neutrino). On associe un
nombre quantique qu’on appelle le nombre leptonique, L, avec chaque
famille leptonique. Pour les anti-leptons, L est opposé.
Seulement l’électron, et les neutrinos sont stables. Pour le µ et le τ-leptons :
€
µ
−→e−
ν
e
νµ
τ
−→e−
ν
e
ντ
τ
−→
µ
−
νµντ
τ
−→h−
ντ etc
On associe à chaque famille une saveur leptonique, avec un nombre
quantique L :
b) Il y a 6 quarks connus; comme les leptons, les quarks sont arrangés en 3
familles. Ils sont les suivants :

4
€
Q= + 2 3 u c t 2 MeV 1.3 GeV 175 GeV
Q=−1 3 d s b 7 MeV 150 MeV 5 GeV
Bu 1 3 0 0
Bc 0 1 3 0
Bt 0 0 1 3
u : up d : down
c : charm s : strange (étrange)
t : top b : bottom ou beauty
Comme dans les cas leptonique, on associe à chaque famille un nombre
quantique de saveur baryonique, B, qui est conservé (sauf mélange des états.
Pour chaque quark, un anti-quark existe ayant la même masse, mais avec la
charge et les autres nombres quantiques interne opposés.
Ce qui est étonnant est l’éventail étendu des masses des neutrinos (très
faibles) jusqu’à t-quark avec une masse de 175 GeV (www.cern.ch/pdg).
Pourquoi la masse, pourquoi le grand éventail de la masse ?
Aucune observation directe d’un quark existe, et selon la théorie de jauge des
interactions fortes (QCD), il n’existe pas dans un état libre.
c) La question que se demande est le comportement des différentes familles des
quarks et des leptons avec les différentes interactions ?
1.2 Les interactions et leurs bosons d’échange
a) La mécanique quantique (les solutions non relativiste de l’équation de
Shroedinger) décrit le mouvement non-relativiste des particules dans un champ
externe. Les théories de champs quantiques décrites le mécanisme de la
transmission d’une force, par l’émission d’un quanta du champ. Selon notre
connaissance, les bosons fondamentaux d’échange, de spin 1, sont émis par une
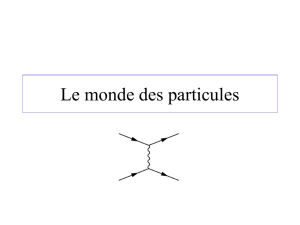
particule de matière, et ensuite absorbé par une autre particule. La figure 1.1
montre l’émission d’un photon par un lepton chargé. La figure 1.2 montre la
vraie interaction entre 2 particules. Les interactions sont faciles à visualiser par
les diagrammes de Feynman. Dans ces diagrammes, les lignes externes sont les
particules réelles. À chaque vertex, l’énergie et l’impulsion sont conservées.
Cela implique que les lignes internes peuvent être virtuels (Appendice 1.1). Au
vertex, il y a un couplage, g, qui se caractérise les différentes forces.
b) Il y a 4 forces (interactions) connues : la force forte, la force faible, la force
électromagnétique, et la force gravitationnelle (Table 1.1). Pour toutes les forces
(avec la possible exception de gravité), l’interaction se porte sur la matière
élémentaire (les fermions) par la transmission d’une particule de jauge (un
boson).

5
Figure 1.1 Emission d’un photon par un fermion (à voir Appendice 2.1)
Figure 1.2 Diffusion de deux électrons (être plus général fermions chargés) par l’échange d’un
photon dans une interaction électromagnétique
FORCE
Gravitation
Électromagnétique
Faible
Forte
PARTICULE
de JAUGE
Graviton
Photon (γ)
W±, Z0
gluon
JP
2+
1–
1– 1+
1–
Masse (GeV)
0
0
MW=80.2
MZ=91.2
0
Portée (m)
∞
∞
10–18
≤10–15
Source
masse
Charge électrique
Charge faible
Charge
couleur
(forte)
Couplage
€
GNM2
4 π c=
5×10−40
€
α =e2
4 πε
0c
=1
137
€
aW=gW
2
4 π c
≈GF(Mc 2)2
(c)3
GF≈10−5
€
α
S≤1
Table 1.1. Les forces connues, et les particules d’échange.
c) La gravité est une interaction qui, à ce jour, n’est pas incluse dans le Modèle
Standard de la physique des particules. La théorie de Relativité Général
d’Einstein est une théorie classique, pour laquelle la source (masse) influence
l’espace-temps. Mais à courte distance, cette théorie devra transformer en
théorie quantique. Un des grands défis des physiciens de la physique des
particules est le développement d’une théorie quantique de jauge pour la gravité.