Corrig - CRDP de l`académie de Montpellier

La stabilité de l’équilibre
Corrigé
Remarque préliminaire
Le prix est à la fois une fonction croissante de la quantité offerte et une fonction décroissante de la
quantité demandée. Les deux courbes présentent forcément un point d'arbitrage déterminant les
paramètres du marché. Cette situation d'équilibre est-elle stable ?
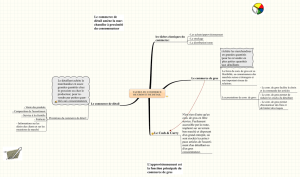
Sur le graphe traditionnel d’Alfred Marshall (prix fonction des quantités), on fait évoluer les variables
de l'échange à partir de leur valeur initiale selon un processus itératif symbolisé par les flèches tracées
en pointillé : prix p1 pratiqué par l’offre à la suite d’un choc exogène → quantité q1 offerte → prix
p2 exigé par la demande pour cette quantité → quantité q2 offerte pour ce prix → prix p3 de la
demande pour cette quantité → quantité offerte q3 pour ce prix → ...
Réponse
1) En situation d'arbitrage, les prix d’offre et de demande sont égaux : 2 O + 2 = - D + 17.
Comme l’offre et la demande sont égales : 2 O + 2 = - O + 17.
On obtient : O = D = 5 unités.
Pour cette quantité, PO = PD = 12 euros.
Pour 20 euros (p1), l’offre se monte à : 20 = 2 O + 2, soit O = 9 (q1).
Pour cette quantité, le prix de demande est : PD = - 9 + 17 = 8 euros (p2).
Pour ce prix, l’offre se monte à : 8 = 2 O + 2, soit O = 3 unités (q2).
Pour cette quantité, le prix de demande est : PD = - 3 + 17 = 14 euros (p3).
Pour ce prix, l’offre se monte à : 14 = 2 O + 2, soit O = 6 unités (q3).
Pour cette quantité, le prix de demande est : PD = - 6 + 17 = 11 euros (p4).
Pour ce prix, l’offre se monte à : 11 = 2 O + 2, soit O = 4,5 unités (q4).
Pour cette quantité, le prix de demande est : PD = - 4,5 + 17 = 12,5 euros (p5).
Pour ce prix, l’offre se monte à : 12,5 = 2 O + 2, soit O = 5,25 unités (q5).
20
10
q4 q3q2
q1 Quantités
Prix de demande
Prix d’offre
Prix
p5
p4
p3
p2
p1
q5 10 20
1

2) En situation d'arbitrage, les prix d’offre et de demande sont égaux : O + 2 = - 2 D + 32.
Comme l’offre et la demande sont égales : O + 2 = - 2 O + 32.
On obtient : O = D = 10 unités.
Pour cette quantité, PO = PD = 12 euros.
Pour 13 euros (p1), l’offre se monte à : 13 = O + 2, soit O = 11 (q1).
Pour cette quantité, le prix de demande est : PD = (- 2 ¯ 11) + 32 = 10 euros (p2).
Pour ce prix, l’offre se monte à : 10 = O + 2, soit O = 8 unités (q2).
Pour cette quantité, le prix de demande est : PD = (- 2 ¯ 8) + 32 = 16 euros (p3).
Pour ce prix, l’offre se monte à : 16 = O + 2, soit O = 14 unités (q3).
Pour cette quantité, le prix de demande est : PD = (- 2 ¯ 14) + 32 = 4 euros (p4).
Pour ce prix, l’offre se monte à : 4 = O + 2, soit O = 2 unités (q4).
Pour cette quantité, le prix de demande est : PD = (- 2 ¯ 2) + 32 = 28 euros (p5).
Pour ce prix, l’offre se monte à : 28 = O + 2, soit O = 26 unités (q5).
P2
30
10
q1q2 q3q4
2010 q5 Quantités
Prix de demande
Prix d’offre
Prix
p5
30
20
p4
p3
p1
3) Dans le premier cas, le prix tend à revenir de lui-même à sa position d'équilibre (stable par
conséquent) ; dans le second, il s'en écarte à chaque période (équilibre instable). L'explication réside
dans la différence de construction des deux schémas. Dans le premier, la valeur absolue de la pente de
la droite du prix d’offre est supérieure à celle de la droite du prix de demande. En termes
économiques, cette remarque signifie que le prix d'offre réagit plus fortement à une variation de la
quantité que celui de la demande, autrement dit que l'élasticité du prix de l'offre à la quantité est
supérieure à celle du prix de la demande (en valeur absolue). Le second schéma représente la
configuration inverse.
2

Enseignements à retirer de cette manipulation
La configuration « explosive » (prix instable) se trouve souvent illustrée par les marchés agricoles
dont la demande est largement incompressible (besoins primaires), d’où d’importantes variations de
prix, à la hausse ou à la baisse en cas de pénurie ou de surabondance, alors que la quantité offerte obéit
davantage aux aléas climatiques et aux délais liés aux cycles naturels qu’aux fluctuations des prix du
marché. Lorsque les deux courbes ont la même pente (en valeur absolue), les augmentations et
diminutions successives de prix sont autoentretenues.
Pour des raisons graphiques évidentes, cette analyse est connue sous le nom anglais de cobweb (toile
d'araignée). On en retiendra la conclusion : le prix est stable si la valeur absolue de l'élasticité du prix
de l'offre est supérieure à celle du prix de la demande ; il est instable dans le cas contraire.
Le cobweb
p4
E
E E
Temps Temps
Prix Prix
O O
Quantités Quantités
Prix Prix
O O
Equilibre stable (A) Equilibre instable (B)
p1
p2
p3
q1
p1
p2
p3
p4
p5
q2 q3 q4
p5
E q1
q2 q3 q4
Offre
Demande
Offre
Demande
q5 E
Quantités
Prix
O
p2
q1 q2
Offre
Demande
p1
E
Temps
Prix
O
Oscillations autoentretenues
Alfred Marshall propose une analyse d'ensemble pour les activités industrielles. Il postule que
l'élasticité du prix de l'offre augmente sous l’effet de la concurrence lorsque le temps de réaction
s'allonge : très faible immédiatement (« période infra-courte »), elle s’accroît dès que le délai est
suffisant pour utiliser des quantités supplémentaires de facteurs dans les installations existantes
(« période courte »), puis devient très élevée quand on peut envisager de bénéficier d’économies
d’échelle grâce à un accroissement des dimensions des entreprises (« période longue »).
Les trois périodes de Marshall
Offre
O
Période infra-courte Période courte
Prix
Quantités
Demande
Offre
O
Période longue
Prix
Quantités
Demande
Offre
O
Prix
Quantités
Demande
3