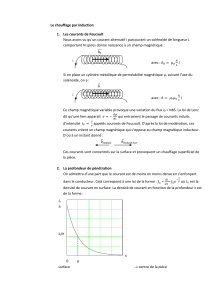
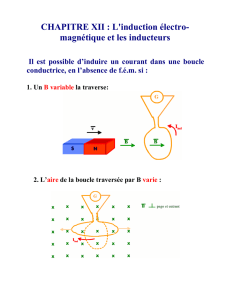
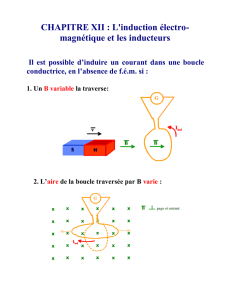
Chauffage par induction électromagnétique : principes

17/09/2008
Madame, Monsieur
Dossier délivré pour
17/09/2008
Madame, Monsieur
Dossier délivré pour
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie électrique D 5 935 − 1
Chauffage par induction
électromagnétique : principes
par Gérard DEVELEY
Ingénieur IEG. Docteur ès sciences
Ancien professeur à l’Université de Nantes
e chauffage par induction électromagnétique fait partie des techniques élec-
trothermiques qui permettent de chauffer un matériau sans contact direct
avec une source d’énergie électrique. Il consiste à plonger le corps à chauffer
dans un champ électromagnétique variable dans le temps, et à dissiper sous
forme de chaleur l’énergie entrant dans le corps. Il se distingue cependant nette-
ment des autres techniques (infrarouge et micro-ondes) par la nature des maté-
riaux chauffés et par la bande de fréquence électrique utilisée, c’est-à-dire par la
profondeur de pénétration et par les densités de puissance de chauffage obte-
nues. En effet, de par son principe, il ne s’applique qu’aux matériaux conduc-
teurs de l’électricité, c’est-à-dire aux matériaux de résistivité électrique comprise
entre 10
–8
Ω.m (cuivre) et 10
–1
Ω.m (verres fondus). La bande de fréquence
employée est comprise entre la fréquence industrielle de 50 Hz et quelques
mégahertz, si bien que les profondeurs de pénétration s’étagent entre quelques
micromètres et quelques centimètres. Les densités de puissance surfacique
peuvent atteindre 10
5
kW/m
2
.
■ On peut caractériser les performances de cette technique de chauffage par le
produit fréquence-puissance et en suivre ainsi l’évolution. Depuis l’époque
où le chauffage par induction faisait appel aux groupes tournants, ce produit a
notablement augmenté. En effet, ces premiers générateurs ont été peu à peu
remplacés par des convertisseurs statiques et, jusqu’à ces dernières années, le
1. Principe et spécificités........................................................................... D 5 935 - 3
2. Quelques rappels théoriques................................................................ — 4
2.1 Transfert électromagnétique entre inducteur et charge........................... — 4
2.2 Effets thermiques......................................................................................... — 10
2.3 Effets mécaniques ....................................................................................... — 12
3. Modélisation numérique des phénomènes couplés....................... — 14
3.1 Généralités ................................................................................................... — 14
3.2 Diverses méthodes numériques de résolution ......................................... — 14
3.3 Algorithmes de couplage............................................................................ — 15
4. Électronique de l’installation ............................................................... — 15
4.1 Système inducteur-charge.......................................................................... — 15
4.2 Circuit oscillant ............................................................................................ — 16
4.3 Alimentation électrique............................................................................... — 19
4.4 Convertisseurs statiques à semi-conducteurs
(basse et moyenne fréquence) .................................................................. — 20
4.5 Générateurs à tube (haute fréquence)....................................................... — 21
Références bibliographiques ......................................................................... –– 22
Pour en savoir plus ............................................................................ Doc. D 5 937
L

17/09/2008
Madame, Monsieur
Dossier délivré pour
17/09/2008
Madame, Monsieur
Dossier délivré pour
CHAUFFAGE PAR INDUCTION ÉLECTROMAGNÉTIQUE : PRINCIPES _______________________________________________________________________________
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
D 5 935 − 2© Techniques de l’Ingénieur, traité Génie électrique
produit fréquence-puissance était classiquement de 100 à 1 000 kHz.kW. Actuel-
lement, la tendance forte est d’augmenter la fréquence et la puissance des ins-
tallations. On peut arriver ainsi à des valeurs fréquence-puissance de l’ordre de
250 000 kHz.kW !! (comme c’est le cas, pour le soudage au défilé des tubes
d’acier ou des torches à plasma inductif de forte puissance).
Tout cela suppose un développement parallèle des matériels électrotechni-
ques nécessaires tels que les condensateurs, les transformateurs, les inducteurs
refroidis par l’eau, le câblage anti-inductif dit couramment « aselfique », etc, qui
constituent la technologie moderne du chauffage par induction.
■ Comme dans tout problème de chauffage, la puissance nécessaire au type
de traitement thermique recherché est imposée par la masse à chauffer, la tem-
pérature à atteindre et le temps de chauffe. Pour l’ingénieur chargé de concevoir
ou de conduire une installation de chauffage par induction, les questions à
résoudre sont d’ordre électromagnétique pour optimiser le transfert de puis-
sance entre la source et le matériau, puis d’ordre thermique pour connaître le
champ de température et son évolution dans le temps.
■ Une fois définie la puissance nécessaire, trois étapes sont en général à fran-
chir.
En premier lieu, se pose la question du choix de la fréquence de travail. En
effet, ce choix conditionne la profondeur de pénétration et permet donc de loca-
liser la source thermique plus ou moins au voisinage de la surface du matériau.
De ce choix dépend la nature du générateur à utiliser.
En second lieu, il faut assurer la maîtrise du transfert entre l’inducteur et le
matériau de façon à obtenir la puissance injectée nécessaire au traitement
recherché. Cette étape permet de définir la forme et la constitution de l’induc-
teur, puis l’adaptation correcte de l’inducteur au générateur.
Enfin, il faut s’assurer que l’évolution des températures et leurs répartitions
dans le matériau correspondent bien au but recherché. Bien que cette dernière
étape relève plus de considérations thermiques qu’électromagnétiques, elle ne
doit pas être négligée. La réussite de l’opération de chauffage en dépend.
L’article « Chauffage par induction électromagnétique » fait l’objet de deux fascicules :
D 5 935 Principes
D 5 936 Technologie
Les sujets ne sont pas indépendants les uns des autres.
Le lecteur devra assez souvent se reporter à l’autre fascicule.

17/09/2008
Madame, Monsieur
Dossier délivré pour
17/09/2008
Madame, Monsieur
Dossier délivré pour
_______________________________________________________________________________ CHAUFFAGE PAR INDUCTION ÉLECTROMAGNÉTIQUE : PRINCIPES
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie électrique D 5 935 − 3
1. Principe et spécificités
La figure 1 montre le schéma de principe d’une installation de
chauffage par induction. On trouve, à partir du réseau électrique
(50 Hz), un convertisseur permettant de créer les courants électri-
ques à la fréquence souhaitée, un adaptateur nécessaire à l’ajuste-
ment des tensions, un inducteur générant le champ électro-
magnétique dans lequel est placée la charge à chauffer.
■Quelques ordres de grandeur sur le chauffage par induction
permettent de mieux cerner ses spécificités.
●Fréquences
Il est habituel de distinguer les plages de fréquences suivantes :
— basse fréquence : de 50 Hz à 1 000 Hz ;
— moyenne fréquence : de 1 000 Hz à 35 kHz ;
— haute fréquence : de 35 kHz à 5 MHz.
●Puissances
On les caractérise par la puissance surfacique
P
s, puissance
injectée dans la pièce rapportée à la surface du matériau.
— Chauffage
pénétrant :
• fréquence : de 1 à 50 kHz pour les métaux et de 0,1 à 4 MHz
pour les semi-conducteurs ;
• puissance : 102 kW/m2 <
P
s < 103 kW/m2 ;
• exemples d’applications : forge, fusion.
— Chauffage
superficiel :
• fréquence : de 10 à 500 kHz pour les métaux ;
• puissance : 5 103 kW/m2 <
P
s < 5 104 kW/m2 ;
• exemples d’applications : trempe superficielle, brasage.
— Chauffage
pelliculaire :
• fréquence : de 10 à 1000 kHz pour les métaux ;
• puissance :
P
s < 105 kW/m2 ;
• exemples d’applications : soudages de tubes, thermoscellage.
L’utilisation d’une fréquence autre que 50 Hz impose de disposer
de générateurs dont le fonctionnement et l’adaptation à la charge
doivent être maîtrisés pour fournir la puissance demandée.
■ Les performances du chauffage par induction se définissent
ainsi par l’association des grandeurs électriques fréquence et
puissance :
●Pour la grosse métallurgie (fusion, réchauffage de brames,
etc.), l’introduction des GTO, des IGBT et la constitution de modules
en parallèle permettent d’obtenir des convertisseurs statiques déli-
vrant quelques mégawatts pour des fréquences allant jusqu’à quel-
ques dizaines de kilohertz.
●Pour les applications de plus faible puissance et nécessitant des
fréquences plus élevées, l’usage de transistors MOS conduit à quel-
ques centaines de kilowatts à quelques centaines de kilohertz.
●Pour les applications sur des matériaux peu conducteurs
(plasma, oxydes métalliques, etc.), le générateur à triode reste
irremplaçable. Les fréquences peuvent être très élevées (typique-
ment de l’ordre du mégahertz), et les puissances sont limitées à
quelques centaines de kilowatts. Les rendements de ces généra-
teurs sont faibles ( < 70 %), ce qui pénalise le rendement global de
l’installation.
Notations et Symboles
Symbole Unité Définition Symbole Unité Définition
a m2.s–1 diffusivité thermique p m profondeur de pénétration
B T induction magnétique P W puissance active électrique
(symbole général) ( P = V I cos ϕ )
c J.kg–1.K–1 capacité thermique massique Q var puissance réactive électrique
( P = V I sin ϕ )
C F capacité du condensateur
(symbole général)
S m2surface du matériau
d m diamètre de l’inducteur T K température (symbole général)
D m diamètre de la charge v m/s vitesse de déplacement de la charge
E V/m champ électrique V volt tension électrique d’alimentation
(valeur efficace) (symbole général)
f Hz fréquence (symbole général) ϕ
0
W.m–2 flux thermique surfacique
F et G nombre facteur de transmission de puissance
active ( F ) et réactive ( G )
λ W.m–1.K–1 conductivité thermique
h W.m–2.K–1 coefficient d’échange superficiel µ H/m perméabilité magnétique ;
dans le vide :
µ
0 = 4π10–7
H A/m champ magnétique µ
r
nombre perméabilité relative ( )
Iampère courant électrique d’alimentation (valeur
efficace) (symbole général)
ρ kg/m3masse volumique
J A/m2densité de courant électrique (symbole
général)
σ S/m conductivité électrique ;
où
ρ (Ω.m) est la résistivité
électrique
L H inductance (symbole général) ω rad/s pulsation ( ω = 2π f )
µ
r
µµ
0
⁄1>=
σ
1
ρ
---=
Figure 1 – Schéma général d’une installation de chauffage
par induction
Convertisseur Adaptateur
Réseau
Corps à chauffer
Inducteur

17/09/2008
Madame, Monsieur
Dossier délivré pour
17/09/2008
Madame, Monsieur
Dossier délivré pour
CHAUFFAGE PAR INDUCTION ÉLECTROMAGNÉTIQUE : PRINCIPES _______________________________________________________________________________
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
D 5 935 − 4© Techniques de l’Ingénieur, traité Génie électrique
2. Quelques rappels
théoriques
2.1 Transfert électromagnétique
entre inducteur et charge
2.1.1 Physique du phénomène
Elle est décrite par les équations de Maxwell dont on donne ici les
formulations adaptées au propos de cet article [1] [2] [3]. Toute
variation d’induction magnétique (
B ) appliquée à un matériau
entraîne la création d’un champ électrique ( E ) qui entraîne à son
tour la création d’un courant électrique (de densité J ) si le matériau
est conducteur de l’électricité.
■La formulation des équations de Maxwell permet de détermi-
ner les diverses grandeurs utiles. Ces dernières sont solutions des
relations suivantes.
●Entre champ électrique E et induction B :
(1)
avec
v vitesse relative de déplacement du matériau par rapport à
l’induction.
Pour une pièce en mouvement lent (chauffage au défilé), le terme
est nul ou négligeable.
●Entre champ magnétique H et densité de courant J :
(2)
en négligeant les courants de déplacement.
■Leur sont associées les relations liées aux propriétés des
matériaux :
●Entre champ électrique et densité de courant :
(3)
où
σ est la conductivité électrique du matériau.
●Entre induction et champ magnétique :
(4)
où
µ est la perméabilité magnétique du matériau.
■Par combinaison de ces équations, et dans le cas simple où la
perméabilité magnétique est constante, on obtient :
(5)
où ∆
B représente le Laplacien de l’induction.
Dans le cas où la variation de
B est sinusoïdale de fréquence f et
pour des corps immobiles, cette relation s’écrit :
(6)
avec j2= –1,
ω pulsation de B (= 2π f ).
La résolution des relations (5) ou (6), associée aux conditions aux
limites de la charge à chauffer, donne la répartition spatiale de
l’induction. La répartition de la densité des courants induits s’en
déduit par les relations (2) et (4).
Il n’est possible de trouver des solutions analytiques que pour des
formes simples (plan, plaque, cylindre ou tube) et pour des maté-
riaux de perméabilité magnétique constante. Dans les autres cas, il
faut avoir recours aux méthodes numériques de résolution de ces
équations (§ 3).
2.1.2 Courants induits dans la charge
(cas d’une plaque semi-infinie)
2.1.2.1 Densité de courant
Dans le cas d’une plaque plane semi-infinie dans la direction
Oz ,
soumise à un champ dirigé suivant Oy , la relation (6) s’écrit :
avec
k
2 =
ωσµ et où H représente le module du champ à la cote z .
La densité de courant s’en déduit par :
,
et a pour module :
(7)
ce qui traduit une variation exponentielle du module de
J à partir de
la surface de la plaque.
J
0 est la densité maximale de courant à la surface du matériau
avec :
,
où
p est la profondeur de pénétration définie au paragraphe 2.1.2.2.
2.1.2.2 Profondeur de pénétration
Pour le cas de la plaque semi-infinie, cette profondeur de pénétra-
tion représente la distance comptée depuis la surface pour laquelle
la densité de courant est égale à
J
0/e (e = 2,718). Elle s’exprime par :
Une formule pratique est :
(8)
dans laquelle
µ
r est la perméabilité magnétique relative du maté-
riau, définie par avec H/m.
Le tableau 1 donne quelques valeurs de
p pour divers matériaux
et diverses fréquences.
Rappelons que conductivité et résistivité électriques sont des
grandeurs inverses. Les électriciens utilisent généralement la
résistivité électrique et la représentent par le symbole
ρ . Ce der-
nier est également celui de la masse volumique et, pour éviter
toute ambiguïté, les formulations sont faites avec la conducti-
vité électrique σ (exprimée en S/m).
rot E ∂
B
∂
t
---------–rot v B ∧()+=
v B ∧
()
rot H J =
J σE =
B µH =
∂ B
∂
t
--------- 1
µσ
------- ∆
B rot v B ∧()+=
∆ B j= ωσµB
La variation de B sinusoïdale de fréquence f est un cas fré-
quent et nous le supposerons vérifié dans la suite des dévelop-
pements.
d2 Hz ()
d
z
2
-------------------j k
2
Hz ()=
J
x
d
Hz ()
d z
----------------
–=
J
x
J
0exp
kz
2
-------
–
=
J
0
kH
02
H
0
p
-------
==
p
2
k
------- 1
π
fσµ
-------------==
p 503 3 1
σµ
r
f
-----------,=
µ
r
µ
µ
0
------= µ
04π10 7–
=

17/09/2008
Madame, Monsieur
Dossier délivré pour
17/09/2008
Madame, Monsieur
Dossier délivré pour
_______________________________________________________________________________ CHAUFFAGE PAR INDUCTION ÉLECTROMAGNÉTIQUE : PRINCIPES
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie électrique D 5 935 − 5
2.1.2.3 Calcul du courant induit pour une plaque
semi-infinie
Au champ inducteur
H
s (valeur efficace de
H à la surface du maté-
riau) correspond le courant induit I
x
, perpendiculaire au plan de la
figure 2. Considérons un trajet fictif ABCD, de largeur unité
défini en bordure du matériau. Ce trajet englobe l’épaisseur p ,
parcourue par le courant I
x
; l’application du théorème d’Ampère le
long d’ABCD conduit à la relation :
.
2.1.3 Puissances induites dans la charge
Elles peuvent se calculer à partir du théorème de Poynting :
où
P est la puissance traversant la surface S du matériau, E
s étant la
valeur (efficace) du champ électrique à la surface du matériau.
En courant alternatif sinusoïdal, le calcul de
P conduit à une
expression complexe de la forme P + j Q où P et Q sont les puis-
sances active et réactive mises en jeu dans le matériau.
Pour la plaque semi-infinie, ces puissances s’expriment par la
relation
(9)
Le calcul de la puissance active dans la profondeur de pénétration
montre qu’elle représente environ 87 % de la puissance totale
induite dans la plaque. Cela montre bien la localisation des sources
thermiques dans la profondeur de pénétration et donne tout son
sens physique à cette dimension a priori arbitraire.
Tableau 1 – Quelques valeurs de la profondeur de pénétration p exprimées en mm, pour une perméabilité relative
(sauf acier à 20 °C)
acier acier cuivre cuivre aluminium aluminium graphite
(
µ
r = 100)
(20 °C) (800 °C) (20 °C) (800 °C) (20 °C) (500 °C) (20-1 300 °C)
f (Hz)
50 3,18 67,2 9,35 19,4 11,9 19,4 201
100 2,25 47,5 6,61 13,4 8,4 13,4 142
1030,71 14,6 2,09 4,26 2,66 4,26 45
1040,225 4,75 0,661 1,34 0,84 1,34 14,2
1050,071 1,46 0,209 0,426 0,266 0,426 4,5
1060,0225 0,475 0,066 0,134 0,084 0,134 1,42
1070,007 0,146 0,021 0,043 0,0266 0,043 0,45
m
r1=
Figure 2 – Calcul du courant induit I
x
<1=
H
sI x
=
P E
s
H
s
∧() S =
PQ
1
σ
---
H
2
s
p
---------
S ==
, = 1
H
s
A
D
B
C
p
I
x
① À partir de la relation (9), on peut voir que la puissance
active transférée au matériau dépend de sa surface externe, de
ses caractéristiques électriques et magnétiques et de la fré-
quence. Si on remplace
p par son expression (8) :
,
on trouve que la puissance s’exprime par la relation
(10)
qui permet un calcul rapide.
② À partir de la relation (9), et en remarquant que le champ
magnétique de surface est donné dans un solénoïde inducteur,
en première approximation, par le théorème d’Ampère
où n est le nombre de spires par mètre et I le courant dans
l’inducteur, on établit que :
.
La charge dans la plaque semi-infinie apparaît comme une
résistance
associée à une inductance
,
soit encore comme une impédance de résistance
R
c et de réac-
tance L
c
ω égales.
p 503 3 1
σ µ
r
f
----------------,=
P 210
3–
H
2
s
1
σ
---
µ
r
f S ⋅=
H
s
n I =
PQ
1
σ
---
n
2
p
------
S I2 ==
R
c1
σ
---
n
2
p
------
S =
L
c1
σ
---
n
2
p
------
S 1
2
πf
---------
=