OG2_Cours_Systèmes Optiques_Miroirs et Lentilles

C
CC
CH10
H10 H10
H10 –
––
– OG2
OG2 OG2
OG2 :
::
: Systèmes Optiques
Systèmes Optiques Systèmes Optiques
Systèmes Optiques –
––
– Miroirs et Lentilles
Miroirs et Lentilles Miroirs et Lentilles
Miroirs et Lentilles –
––
– 1/
1/ 1/
1/1
11
14
44
4
Premières Définition
Premières DéfinitionPremières Définition
Premières Définitions
ss
s :
::
:
Système Optique
Système OptiqueSystème Optique
Système Optique :
::
: E
EE
Ensemble de surfaces réfractantes (dioptres) et réfléchissantes (catadioptres)
nsemble de surfaces réfractantes (dioptres) et réfléchissantes (catadioptres) nsemble de surfaces réfractantes (dioptres) et réfléchissantes (catadioptres)
nsemble de surfaces réfractantes (dioptres) et réfléchissantes (catadioptres)
permett
permettpermett
permettant
antant
ant l’observation indirecte d’un objet, en formant une image.
l’observation indirecte d’un objet, en formant une image. l’observation indirecte d’un objet, en formant une image.
l’observation indirecte d’un objet, en formant une image.
Objectif du chapitre
Objectif du chapitreObjectif du chapitre
Objectif du chapitre :
::
:  Etude des systèm
Etude des systèm Etude des systèm
Etude des systèmes optiques les plus courants
es optiques les plus courantses optiques les plus courants
es optiques les plus courants
(Miroirs, Lentilles et Associations)
(Miroirs, Lentilles et Associations)(Miroirs, Lentilles et Associations)
(Miroirs, Lentilles et Associations)
Définitions
DéfinitionsDéfinitions
Définitions :
::
:
Remarque : Un objet (ou une image) est dit étendu, si il (elle) est constitué(e) de plusieurs points
Point Objet
Point ObjetPoint Objet
Point Objet :
::
:
Intersection de rayons lumineux
arrivant dans le système optique
Point
Point Point
Point Image
ImageImage
Image :
::
:
Intersection de rayons
lumineux sortant du
système optique
Peut émettre directement
sa propre lumière
(Objet physi
que réel)
A’
Syst
A
Syst
Ou n’être que l’intersection de rayons
(Par exemple l’image d’un système
précédent – Sans réalité physique)
A
Syst
2
Syst
1
Objet
ObjetObjet
Objet
Image
ImageImage
Image
Ex
ExEx
Ex
:
::
:  Miroir
 Télescope
 Microscope
 L’œil / La loupe
 Lunette / Lentille
 Génère
l’information
lumineuse
 Reproduction de
l’objet lumineux par
le système optique
Système
SystèmeSystème
Système
Optique
OptiqueOptique
Optique
Forcément généré par
un système optique…

I
II
I Le
Le Le
Le Miroir
Miroir Miroir
Miroir P
PP
Plan
lanlan
lan
Miroir plan = Surface Plane réfléchissante
I.1
I.1I.1
I.1 Construction de l’image
Construction de l’imageConstruction de l’image
Construction de l’image (
( (
(Voir
VoirVoir
Voir TP)
TP) TP)
TP)
 On applique les lois de Snell-Descartes : r = -i
 On cherche l’intersection des rayons émergents
 Ils se croisent AVANT la face de sortie du miroir
 Les rayons semblent provenir de A’, symétrique
de A par rapport au plan du miroir.
I.2
I.2I.2
I.2 Notion d
Notion dNotion d
Notion de réel et de virtuel
e réel et de virtuele réel et de virtuel
e réel et de virtuel
2
2 2
2 TYPES d’IMAGES
TYPES d’IMAGESTYPES d’IMAGES
TYPES d’IMAGES
De la même manière pour un objet :
2
2 2
2 TYPES d’OBJETS
TYPES d’OBJETSTYPES d’OBJETS
TYPES d’OBJETS
I.3
I.3I.3
I.3 Relation de Conjugaison
Relation de ConjugaisonRelation de Conjugaison
Relation de Conjugaison
Relation donnant la position de l’image A’ en fonction de celle de l’objet A.
On dit que A et A’ sont conjugués par le système optique.
Ici, A’ est le symétrique de A par rapport au plan du miroir :
HA HA
′
= −
(avec H projeté ortho de A)
Syst
A’
Oeil
A’
Syst
Ecran pour
la visualiser
Oeil
A’
A
Système Optique
Syst
A
S
2
A
S
1
OBJET
OBJET OBJET
OBJET R
RR
REEL
EELEEL
EEL
Intersection des rayons AVANT
la face d’entrée du système
Cas de tous les objets concrets
OBJET VIRTUEL
OBJET VIRTUELOBJET VIRTUEL
OBJET VIRTUEL
Intersection des rayons APRES
la face d’entrée du système
 Ne peut être que
l’image réelle d’un syst
optique S 1 précédent
IMAGE VIRTUELLE
IMAGE VIRTUELLEIMAGE VIRTUELLE
IMAGE VIRTUELLE
Le croisement des rayons se fait
AVANT la face de sortie du système
L’image semble provenir de derrière la face
de sortie du système, l’endroit d’où elle
semble provenir n’a pas de réalité matérielle
Remarque : Seul
l’œil ou un autre système
optique peut voir l’image (on peut l’observer,
la photographier, mais pas l’afficher
directement sur un écran)
IMAGE REELLE
IMAGE REELLEIMAGE REELLE
IMAGE REELLE
Le croisement des rayons se fait
APRES la face de sortie du système
L’endroit où l’image se forme est bien réel,
bien matérialisable. Si on place la main ou
un écran sur A’, on voit l’image apparaître.
Remarque
: L’œil peut aussi voir directement
l’image s’il est placé APRES à au moins 25cm
A
Syst
A’
Image Virtuelle
Objet
Réel
i
r
A
H
Rayons
émergents
Rayons
incidents
Image =
Croisement
des Rayons
émergents
(CH10
(CH10 (CH10
(CH10 –
––
– OG
OG OG
OG2
22
2 –
––
– 2
22
2/
//
/14
1414
14)
))
)

II
IIII
II S
SS
Système optiq
ystème optiqystème optiq
ystème optique
ueue
ue centré
centré centré
centré
II.1
II.1II.1
II.1 Définition
DéfinitionDéfinition
Définition
Déf : Un système optique est dit centré s’il
présente un axe de symétrie de révolution.
(Système invariant par rotation autour de cet axe)
Cet axe est appelée l’AXE OPTIQUE du système
Cet axe est appelée l’AXE OPTIQUE du systèmeCet axe est appelée l’AXE OPTIQUE du système
Cet axe est appelée l’AXE OPTIQUE du système
Remarque : L’axe optique est perpendiculaire à toutes les surfaces réfractantes ou réfléchissantes du système
Conséquence : Un rayon arrivant suivant l’axe optique d’un système centré n’est pas dévié par celui-ci
Vocabulaire : Deux directions caractéristiques
II.2
II.2II.2
II.2 Stigmatisme
Stigmatisme Stigmatisme
Stigmatisme
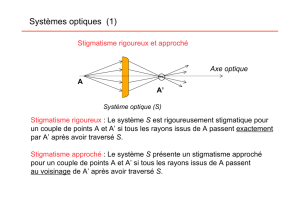
Principe : Pour qu’une image soit nette, il faut que la lumière provenant d’un point objet A ne se concentre
qu’en UN U NIQUE PO INT IMA GE A’
Définition : Un système est dit S TIG MA TIQU E
STI GMATIQ UESTI GMATIQ UE
STI GMATIQ UE si il fait converger tous les
rayons émergents d’un point objet A vers un unique point image A’.
Remarque : Le stigmatisme est une condition essentielle pour avoir un bon système optique
Mais LE SEUL SYSTEME RIGOUREUSEMENT STIGMATIQUE est le MIROIR PLAN…
STIGMATISME APPROCHE
STIGMATISME APPROCHESTIGMATISME APPROCHE
STIGMATISME APPROCHE :
::
: Pour les autres, on doit se satisfaire en général d’un stigmatisme approché
En effet, pour obtenir une bonne image, il suffit que la zone image (région où se croisent les rayons
émergents depuis un point objet A) soit inférieure à la taille d’une cellule de l’œil, ou à la taille d’un pixel
(pour un capteur numérique).
II.3
II.3II.3
II.3 Aplanétisme
AplanétismeAplanétisme
Aplanétisme
Pour que l’observation d’objets étendus soit possible, il faut que cette
propriété de stigmatisme se conserve dans tout le plan transverse
(par exemple sur toute la surface d’une photo…)
Déf : Un système est dit APL ANET IQUE
APLANET IQUEAPLANET IQUE
APLANET IQUE si le stigmatisme
pour tout couple (A, A’) de l’axe optique se conserve pour
tout couple (B, B’) dans les plan transversaux.
Autrement dit : L’image de tout plan transverse est également un plan transverse
Lentille
Miroir Sphérique
Autres exemples :
 Miroirs
Paraboliques
Tous les rayons se croisent en un seul point,
la lumière est concentrée, l’image est nette
Tous les rayons ne se croisent pas en un seul point,
mais en une zone image, l’image est floue
Syst
SystSyst
Syst
Zone Image A’
Exemples
:
Direction
“
Axiale
”
Direction
“Transversale”
A’
Syst
SystSyst
Syst
SYSTEME ST IG MA TIQU E
SYSTEME ST IG MA TIQU ESYSTEME ST IG MA TIQU E
SYSTEME ST IG MA TIQU E
:
::
:
SYSTEME NO N STIGMA TIQU E
SYSTEME NO N STIGMA TIQU ESYSTEME NO N STIGMA TIQU E
SYSTEME NO N STIGMA TIQU E
:
::
:
Syst
SystSyst
Syst
Zone
Image
Illustration sur Capteur
numérique 5*5 = 25 pixels
Stigmatisme Approché
Satisfaisant  Image nette
Système NON Stigmatique,
ou Astigmate  Image floue
B
Syst
SystSyst
Syst
A
B’
A’
Plan
Objet
Plan Image
(CH10
(CH10 (CH10
(CH10 –
––
– OG
OG OG
OG2
22
2 –
––
– 3
33
3/
//
/14
1414
14)
))
)

Page laissée intentionnellement blanche
(CH10
(CH10 (CH10
(CH10 –
––
– OG
OG OG
OG2
22
2 –
––
– 4
44
4/
//
/14
1414
14)
))
)

III
IIIIII
III Lentilles Sphériques Minces
Lentilles Sphériques MincesLentilles Sphériques Minces
Lentilles Sphériques Minces
III.1
III.1III.1
III.1 Présentation
Présentation Présentation
Présentation et Modélisation
et Modélisationet Modélisation
et Modélisation
Déf : Lentille Sphérique = portion de MHTI comprise
entre deux surfaces sphériques présentant un axe de
révolution commun.
Cas particulier : Lentille Sphérique Mince, si
1
2
e D
e R
e R
≪
≪
≪
Modélisation :
Types de lentilles : C
CC
CONVERGENTES
ONVERGENTESONVERGENTES
ONVERGENTES D
DD
DIVERGENTES
IVERGENTESIVERGENTES
IVERGENTES
Exemple de lentilles courantes :  Loupes
 Verres de lunettes, lentilles de contact …
III.2
III.2III.2
III.2 Condition
ConditionCondition
Conditions
ss
s de Gauss
de Gauss de Gauss
de Gauss
Le seul système optique parfaitement stigmatique est le miroir plan. La lentille est donc non stigmatique.
Mais il suffit d’avoir un stigmatisme approché pour obtenir des images nettes.
Avec les lentilles minces, il faut limiter les conditions d’utilisation pour conserver un stigmatisme approché
Conditions de Gauss
Conditions de GaussConditions de Gauss
Conditions de Gauss :
::
: On se limite aux Rayons PARAXIAUX  Proches de l’axe optique
 Faiblement inclinés
Dans l es con di tions de G auss, une l en ti lle m ince prés ente
Dans l es con di tions de G auss, une l en ti lle m ince prés ente Dans l es con di tions de G auss, une l en ti lle m ince prés ente
Dans l es con di tions de G auss, une l en ti lle m ince prés ente
un s tigma tisme a pproché et un aplan ét is me approc
un s tigma tisme a pproché et un aplan ét is me approcun s tigma tisme a pproché et un aplan ét is me approc
un s tigma tisme a pproché et un aplan ét is me approch é
héhé
hé
Conséquences mathématiques :
 Lentille mince : e << R 1 , e << R 2 e << d
La lentille peut-être supposée plane, réduite à son plan tangent, O = S 1 = S 2
Tous les calculs se font dans des triangles rectangles (voir pages suivantes)
 Rayons faiblement inclinés,
En général, on prend α < 10° (selon la précision voulue) :
Bi
-
convexe
Plan
Convexe
Ménisque
Convergent
Modélisation
Bi
-
concave
Plan
Concave Ménisque
Divergent
S
1
S
2
e
R
2
R
1
D
Courbure
Plan Tangent
O
O = Centre optique de la lentille
(Les sommets S 1 et S 2 sont quasiment confondus)
Modélisation
sin
cos 1
tan sin
α α
α
α α α
≈
≈
≈ ≈
(CH10
(CH10 (CH10
(CH10 –
––
– OG
OG OG
OG2
22
2 –
––
– 5
55
5/
//
/14
1414
14)
))
)