Annales 2008 à 2010

PHY 241 ANNALES (responsable UE : P. Toulemonde)
1
UE PHY241 DLST - U. J. Fourier
Année 2010/11
Annales
Ce document contient les annales de PHY241 des épreuves terminales (sessions 1 et 2) pour les années
2008-09 et 2009-10.

1
Licence de Sciences et Technologie – 2ème année année 2008-09
UE PHY241
Epreuve terminale (durée 2h)
Documents interdits – Calculatrice interdite
QUESTION DE COURS (~ 30 min) :
1 – Rappeler l’expression de la force de Laplace en précisant chacun des termes et son cadre
d’application.
2 – Pendule électrique :
On considère un conducteur filiforme cylindrique rigide de longueur l de masse m mobile
autour d’un axe horizontal perpendiculaire au fil en une de ses extrémités (point O). L’autre
extrémité affleure dans du mercure contenu dans une cuve. Un courant d’intensité I constant
traverse le fil dans le sens imposé par le générateur du schéma ci-dessous. Le fil est placé dans
un champ magnétique
B
uniforme perpendiculaire au plan de la figure.
(a) Déterminer à l’équilibre l’angle d’inclinaison α du fil par rapport à la direction
verticale en fonction de B, I, l, m et g, le fil affleurant exactement à la surface du
mercure à l’équilibre. A-t-on le même équilibre si on applique un courant I dans le sens
opposé ?
(b) On appelle Φ0 le flux embrassé de
B
à travers le circuit lorsque I = 0, c'est-à-dire
lorsque
α = 0. A partir de la situation précédente à l’équilibre, on diminue le courant I
de dI. Donner la variation du flux d Φ associée en fonction de B, l et α . En déduire la
force électromotrice (fem) induite si la diminution de I s’effectue pendant un temps dt.
α
B
mercure
Ο

2
PROBLEME (~ 1h30) : Ampèremètre à pince
Un barreau cylindrique conducteur (C), infiniment long, de section droite s =
π a2 (un disque) et
d’axe zz’ est constitué d’un métal de conductivité
γ . Il est parcouru par un courant électrique
continu d’intensité I, de densité uniforme jparallèle à z’z.
I. Cylindre conducteur
1 – Faire un schéma et analyser les symétries de la distribution de courant du système. En
déduire, dans un système de coordonnées adapté, l’orientation du champ magnétique
)(MB créé par ce courant I en un point M de l’espace et sa dépendance par rapport aux
variables.
2 – Appliquez le théorème d’Ampère pour déterminer )(MB en tout point M de l’espace. On
distinguera deux cas possibles. Tracer l’allure de la fonction )(MB .
3 – (a) Sachant que la puissance P dissipée par effet Joule et par unité de volume est
γτ
2
j
d
dP =,
montrer que la résistance électrique d’une longueur l du cylindre s’écrit : 2
a
l
R
γπ
=
(b) [« points bonus » !] Comparer cette puissance P dissipée dans une longueur l du
conducteur au flux du vecteur de Poynting
P
à travers sa surface latérale. On rappelle que
0
μ
BE
P∧ =et que Ej
γ =.
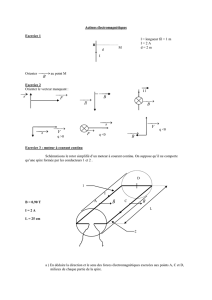
II. Tore de section carrée
Une surface torique, de section carrée est engendrée par un
carré de coté 2b tournant autour d’un axe (
Δ) de son plan,
parallèle à deux de ses cotés. On réalise un solénoïde
torique (S) en enroulant un fil conducteur sur la surface
précédente, de manière à constituer une seule couche de N
spires identiques carrées jointives supposées planes.
Désignons par c le rayon moyen de ce solénoïde (voir
figure ci-contre représentant une partie du solénoïde). Un
courant continu d’intensité I’ circule dans les spires.
(
Δ
)
c 2b
(S)
N spires
juxtaposées

3
1 – En vous aidant de schémas (vues en coupe ou en 3D), indiquez les symétries de la
distribution de courant I’ et en déduire l’orientation du champ magnétique )(MB en un point M
de l’espace engendré par la circulation de I’.
2 – Déterminer le champ )(MB à l’intérieur et à l’extérieur de (S) crée en un point M à une
distance ρ’ de l’axe (Δ). En particulier montrer que ce champ est nul pour M extérieur au tore.
3 – Exprimer l’énergie emmagasinée Em dans tout le volume du tore. On rappelle que l’énergie
emmagasinée par unité de volume d’un système générant un champ
B
est donné par
l’expression
0
2
2 μτ
B
d
dEm=.
4 – Déduire de l’expression précédente que l’inductance propre (coefficient d’auto-induction)
du tore est : ⎟
⎠
⎞
⎜
⎝
⎛
−
+
=bc
bc
bN
Lln
2
0
π
μ
. Retrouvez ce résultat en calculant le flux propre de
B
à
travers 1 spire constitutive du tore puis à travers ses N spires.
III. Association des 2 systèmes
On considère à présent le système formé par l’association du cylindre conducteur (C) de
longueur infinie, parcouru par un courant I et le solénoïde torique (S) dont on réunit maintenant
les extrémités du fil entre elles (I’ = 0), de manière à constituer un circuit fermé. Les axes zz’ et
(
Δ ) des deux sous-systèmes sont confondus.
1 – Montrer que l’expression littérale du coefficient d’induction mutuelle Mspire entre (C) et une
spire de (S) s’écrit ⎟
⎠
⎞
⎜
⎝
⎛
−
+
=bc
bc
b
Mspire ln
0
π
μ
. En déduire la valeur de la mutuelle M du système
complet.
2 – Si l’intensité I du courant dans le cylindre diminue à partir de sa valeur initiale, que se
passe-t-il dans le circuit du tore ? I’ reste-t-il nul ? Sinon, dans une figure en coupe (passant par
l’axe z’z) précisez son sens en justifiant votre réponse.
3 – On reprend le dispositif ci-dessus en reliant maintenant les extrémités du bobinage torique
aux bornes d’un voltmètre et en injectant dans le cylindre (C) un courant )cos(
0tII
ϖ
=, qui
varie donc dans le temps.
(a) Qu’observe-t-on sur le voltmètre ? Calculer l’amplitude e0 de la force électromotrice (fem)
d’induction dans le solénoïde.
(b) Ce dispositif est utilisé dans l’industrie sous le nom « d’ampèremètre à pince ». Quel est
l’intérêt de ce montage ?

1
Licence de Sciences et Technologie – 2ième année année 2008-09
UE PHY241
Epreuve terminale, session 2 (durée 2h)
Documents interdits – Calculatrice interdite
QUESTIONS DE COURS & APPLICATION DU COURS (~ 40 min) :
1. On considère un condensateur plan aux armatures infinies (dans les directions x et y),
chargé, à l’équilibre (cf. schéma ci-dessous).
a) Quelle est la densité de charges volumique dans ses armatures (justifier)? Pourquoi a-
t-on à l’équilibre des densités de charges opposées entre les armatures ? Que vaut le
champ électrostatique à l’intérieur des armatures ?
Calculez le champ électrostatique créé entre les armatures infinies de ce condensateur
plan, en fonction de la densité surfacique de charges
σ et de la distance d entre ses
armatures.
b) En l’absence de champ magnétique, les deux premières équations de Maxwell
s’écrivent
0
ε
ρ
=Ediv
r
et 0
r
r
r
=Etor
Sans démonstration, donnez les formes intégrales (et leurs noms) de ces deux équations
avec leurs conditions d’utilisation.
c) Retrouvez l’expression des opérateurs divergence et rotationnel en coordonnées
cartésiennes. Montrez alors que les deux premières équations de Maxwell sont vérifiées
dans l’espace entre les deux armatures chargées.
x y
z
O+
σ
-
σ
d