Propagation de la lumière

Chapitre II page II-1
II. PROPAGATION DE LA LUMIERE
Le rayon lumineux est la notion fondamentale de l’optique géométrique. Nous allons étudier la
propagation de la lumière, c’est à dire la forme des rayons lumineux et la célérité de la lumière.
A. Premières notions d’optique géométrique
1. Faisceau et pinceau lumineux
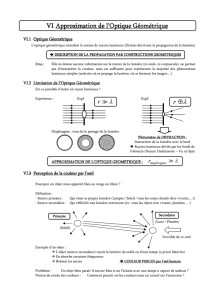
Lorsqu’on s’éclaire avec une lampe de
poche, on voit dans la nuit le faisceau
de lumière émis par la lampe. Lorsque
le faisceau est moins large, on parle de
pinceau lumineux.
2. Rayon lumineux et loi d’indépendance
Le rayon lumineux est le modèle de la lumière en optique géométrique.
L’intérêt de cette notion est de permettre d’expliquer le
comportement des faisceaux lumineux { l’aide de lois simples
concernant le comportement d’un rayon lumineux.
En optique géométrique, un faisceau lumineux est considéré comme
formé d’une infinité de rayons lumineux.
Ces rayons lumineux n’interagissent pas les uns avec les autres. Ils se propagent dans un milieu
et éclairent une surface (un écran ou la rétine) indépendamment les uns des autres.
B. Loi de propagation rectiligne de la lumière
1. Histoire
Dès le IIIe siècle avant notre ère, la loi de propagation rectiligne du rayon visuel était acquise.
Elle était énoncée de cette manière : un rayon visuel a la même forme qu’un fil tendu, c’est { dire
celle d’une droite. Cet énoncé est un peu différent de ce que nous connaissons car il décrit le
rayon visuel (hypothétique et émis par l’œil) et non le rayon lumineux.
fig. 2.2 :
quelques rayons lumineux
appartenant à un faisceau
fig. 2.1 : faisceau et pinceau lumineux
faisceau lumineux
source lumineuse
pinceau lumineux

Chapitre II page II-2
2. Définitions
Un milieu transparent se laisse traverser par la lumière. (Le contraire de transparent est
opaque.)
Un milieu homogène possède la même composition chimique en chacun de ses points.
Un milieu isotrope est un milieu dans lequel toutes les directions sont équivalentes. (Le
contraire d’isotrope est anisotrope.)
3. Enoncé
Dans un milieu transparent, homogène et isotrope, la propagation de la lumière est rectiligne ;
les rayons lumineux sont des droites.
4. Remarques
Dans un milieu transparent inhomogène, les rayons lumineux sont incurvés. C’est ce qui
explique les mirages, et les miroitements qu’on observe sur une route en été.
Le spath d’Islande est un exemple de milieu transparent, homogène et
anisotrope. Un rayon lumineux entrant dans un tel cristal se scinde en
deux rayons, l’un est dit ordinaire, l’autre extraordinaire. Lorsqu’on
pose un spath d’Islande sur une ligne d’écriture, on la voit en double.
C. Loi du retour inverse de la lumière
1. Enoncé
Lorsqu’un rayon lumineux peut cheminer d’un point A à un point B, alors un rayon lumineux
peut aussi cheminer du point B au point A en suivant le même trajet en sens inverse.
2. Remarque
La loi de propagation rectiligne de la lumière est, de façon manifeste, compatible avec la loi du
retour inverse.
D. Célérité de la lumière
1. Célérité de la lumière dans le vide
Les Hommes ont d’abord cru que la célérité de la lumière était infinie car les phénomènes
lumineux paraissent instantanés. Mais au XVIIe siècle, en 1676, Römer (astronome danois 1644-
1710) découvre, grâce à ses observations des satellites de Jupiter, que la célérité de la lumière
est finie et en effectue la première mesure, 214 000 km/s. Ce résultat n’est pas excellent, mais
l’ordre de grandeur est bon. Par la suite les mesures s’améliorent et donnent
c 300 000 km/s 3. 108 m/s.
optique géométrique
optique géométrique
fig. 2.3 : deux mots vus
à travers un spath d'Islande

Chapitre II page II-3
La valeur actuelle est fixée à 299 792 458 m/s et est devenue une constante du système
international d’unités car la définition du mètre en découle : le mètre est la distance parcourue
par la lumière dans le vide en 1/299 792 458 seconde.
2. Célérité de la lumière dans les autres milieux
Dans tout autre milieu, la mesure de la célérité v d’une lumière monochromatique (d’une seule
couleur) montre qu’elle est inférieure { la célérité c de la lumière dans le vide :
c
vn
avec n supérieur à 1. Cette relation définit le nombre n :
c
nv
Il est appelé indice de réfraction du milieu. Etant le quotient de deux vitesses, c’est un nombre
sans unité. Dans un milieu transparent, homogène et isotrope l’indice de réfraction est
uniforme : il a la même valeur en chacun des points du milieu.
3. Dispersion : influence de la fréquence de l’onde sur sa célérité
Chaque onde monochromatique (d’une seule couleur) est caractérisée par une fréquence f (ou
une période T = 1/f).
Dans certains milieux, la célérité d’une onde monochromatique ne dépend pas de sa fréquence.
Ces milieux sont dits non dispersifs. C’est le cas du vide et de l’air.
Dans les milieux dispersifs, comme le verre ou l’eau, la célérité v de la lumière dépend du milieu
et aussi de la fréquence de l’onde. Donc l’indice du milieu dépend de la fréquence de l’onde.
De la lumière blanche se propageant dans le vide et arrivant dans un milieu comme le verre s’y
disperse : chacune des couleurs se propage avec une célérité différente. Nous aurons l’occasion
de revenir sur ce phénomène de dispersion en étudiant le prisme.
4. Quelques valeurs de l’indice de réfraction
Indice de l’air : n = 1,000293. La propagation de la lumière est presque aussi rapide dans l’air
que dans le vide. Sauf indication contraire, nous prendrons l’indice de l’air égal { 1.
Indice de l’eau : n = 1,33. C’est une valeur moyenne, cet indice varie avec la fréquence de l’onde.
Indice du verre courant (dit crown) : n = 1,5. C’est une valeur moyenne, cet indice varie suivant
la nature du verre et la fréquence de l’onde.
Indice du verre de cristal (dit flint) : n = 1,7. Même observation que pour le verre ordinaire.

Chapitre II page II-4
5. Influence du milieu sur la longueur d’onde
La longueur d’onde est la distance que parcourt une onde monochromatique en une période.
De ce fait, dans le vide la longueur d’onde est donnée par :
0cT
et dans un milieu d’indice n par :
vT
.
Cette grandeur est donc caractéristique de l’onde (par sa période T ou sa fréquence f = 1/T) mais
aussi du milieu (par la célérité v) :
0
c
vT T
nn
6. Ordre de grandeur des longueurs d’onde et des fréquences lumineuses
La longueur d’onde dans le vide n’est fonction que de la fréquence f de l’onde (ou de sa période
T = 1/f). C’est pourquoi nous pouvons choisir de caractériser une onde monochromatique par sa
longueur d’onde dans le vide plutôt que par sa fréquence.
Les longueurs d’onde 0 de la lumière visible dans le vide s’échelonnent de 400 { 800 nm
environ. Les fréquences correspondantes sont de l’ordre de 1014 Hz. On préfère généralement
utiliser les longueurs d’onde pour caractériser une lumière monochromatique car leurs valeurs
sont plus faciles à manier que celles des fréquences.
L’ordre de grandeur des longueurs d’onde = 0/n de la lumière visible dans l’air est le même
puisque l’indice de réfraction de l’air est très proche de 1.
E. Limite de validité de l’optique géométrique
1. Diffraction
Lorsqu’un faisceau lumineux rencontre un obstacle, il est diffracté par cet obstacle, c’est { dire
que la direction de propagation est modifiée par l’obstacle.
On utilise régulièrement ce phénomène quand il s’agit d’ondes sonores : on entend facilement ce
qu’il se passe dans une pièce dont la porte est ouverte ou entrouverte, même en n’y étant pas et
même en ne se plaçant pas juste devant la porte. La vitesse du son est d’environ 340 m/s, la
fréquence du la 440 est 440 Hz, donc la longueur d’onde vaut environ :
340 0,8
440
v
vT m m
f
Ce résultat est comparable à la largeur de la porte.

Chapitre II page II-5
L’expérience montre que la diffraction s’observe nettement quand les dimensions de l’obstacle
sont du même ordre de grandeur que la longueur d’onde. Cette constatation est valable aussi
pour la lumière.
2. L’optique géométrique
En optique géométrique, on est placé dans des conditions telles que les obstacles sont grands
devant la longueur d’onde. En effet la dimension caractéristique D d’un système optique (un
objectif d’appareil photo par exemple) est de quelques cm, tandis que la longueur d’onde de la
lumière visible est de quelques centaines de nm, donc : D >> .
La diffraction est alors négligeable et la loi de propagation rectiligne de la lumière s’applique.
Après avoir introduit la notion de rayon lumineux, nous avons rencontré les deux premières lois de
l’optique géométrique : la propagation rectiligne de la lumière et la loi du retour inverse.
La propagation de la lumière s’effectue à 300 000 km.s-1 dans le vide. Cette célérité dépend du
milieu de propagation et, dans les milieux dispersifs, de la fréquence de l’onde.
Dans un milieu transparent, homogène et isotrope, la propagation rectiligne de la lumière est
valable lorsque la diffraction est négligeable, c’est à dire lorsque la dimension des obstacles est très
supérieure à la longueur d’onde de la lumière.
Dans le chapitre suivant, nous étudierons ce qui arrive à un rayon lumineux lorsqu’il doit passer
d’un milieu transparent à un autre.