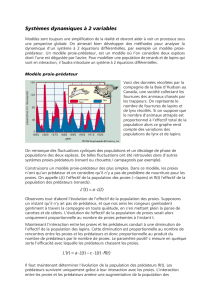
La sensibilité aux conditions initiales

La sensibilité aux conditions initiales
En mathématiques, une suite est obtenue en calculant la valeur d'un nombre
en fonction d'un autre. Par exemple, la suite 1, 2, 4, 8, 16,32, ... est obtenue
en multipliant par 2le nombre précédent. On écrira que le nombre de rang
n+ 1 est égal à 2 fois le nombre de rang n,ou encore que Xn+1 = 2 × Xn.
Exemples
La suite
logistique
La suite logistique est la suite :
Xn+1 = a×Xn× (1 –Xn)
avec 0 ≤a≤4et 0≤X0≤1
a = 2
a = 3,2
a = 3,5
a = 3,6
0.3 - 0.42 - 0.4872 - 0.4997 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5 - 0.5
0.5 - 0.8 - 0.512 - 0.7995 - 0.5129 - 0.7995 - 0.513 - 0.7995 - 0.513 - 0.7995 - 0.513 - 0.7995 - 0.513 - 0.7995 - 0.513
0.5 - 0.875 - 0.3828 - 0.8269 - 0.5009 - 0.875 - 0.3828 - 0.8269 - 0.5009 - 0.875 - 0.3828 - 0.8269 - 0.5009 - 0.875
0.5 - 0.9 - 0.324 - 0.7885 - 0.6004 - 0.8637 - 0.4238 - 0.8791 - 0.3827 - 0.8505 - 0.5302 - 0.8967 - 0.3334 - 0.8001
T
2T
4T
chaos
a = 2
a = 3,2
a = 3,5 a = 3,6
2 4
3
a
T2T 4T
8T
3T
CHAOS
www.physifolies.fr
flashez ce code pour jouer avec le chaos
a = 3,9
X0= 0,3
X’0= 0,300001

Comme toujours en physique, on cherche à reproduire des comportements
en simplifiant à l’extrême le système. On suppose que :
Les hypothèses de départ
pour les loups et les renards
proies
prédateurs
www.physifolies.fr
1. Les renards ont une source illimitée de nourriture.
2. Le nombre de naissances chez les renards est proportionnel au
nombre de renards, mais sature quand il y a trop de renards
3. Les renards ne meurent jamais autrement que tués par un loup.
4. Le nombre de renards tués est proportionnel au nombre de rencontres
d’un loup et d’un renard.
5. Les loups ne meurent que de mort naturelle.
6. Le nombre de morts chez les loups est proportionnel au nombre de
loups.
7. Le nombre de naissances chez les loups est proportionnel à la
nourriture ingérée.
La traduction mathématique
Le modèle continu
Nombre de renards : x
Nombre de loups : y
Variation du nombre de renards : 
Variation du nombre de loups : 
Loup Renard Lapin Herbe
Requin Cabillaud Bdellovibrio Photobactérium
La traduction mathématique
Le modèle discret
On calcule xet yàdes intervalles de temps réguliers
(par exemple, tous les jours). On doit donc déterminer
le nombre d’animaux au jour n+1 en fonction du
nombre au jour n.En s’inspirant du modèle ci-
dessous, on obtient une suite à 2 dimensions :
L’évolution des populations
en fonction du temps
modèle
continu
modèle
discret
Pour la plupart des paramètres, on trouve un comportement différent
dans les deux modèles car ils ne sont pas équivalents.
Le modèle discret présente des régimes chaotiques. Le modèle continu
ne peut pas être chaotique, car il n’y a que 2 variables (2 degrés de
liberté), et que 3 au minimum sont nécessaires pour avoir du chaos.
Le modèle discret est équivalent au modèle continu
pour des valeurs de (1-a),b, (c+1) et dtrès petits.
Deux proies et un prédateur
Dans ce modèle, on rajoute une espèce supplémentaire à celles du
modèle proie-prédateur traditionnel. Il s’agit d’une proie pour les deux
premières espèces. Ce sera par exemple le lapin, qui est une proie
pour le loup et le renard. Dans ce modèle, les populations peuvent
évoluer de façon chaotique.
La traduction mathématique
Le modèle Monte-Carlo
On divise le territoire en cases (par exemple, 1000 x
1000 cases). Une case peut être vide, contenir un
loup ou contenir un renard. Puis on fait se déplacer
aléatoirement les loups et les renards sur le territoire.
Si un loup et un renard tombent sur la même case, le
loup tue le renard, et un louveteau nait, avec une
certaine probabilité. On introduit aussi une probabilité
qu’un renard apparaisse spontanément dans une case
vide, et qu’un loup meurt. En moyenne, ce modèle est
équivalent au modèle continu.
Flasher ce code pour
jouer avec le chaos

Le chaos
www.physifolies.fr
Le chaos déterministe, qu’est-ce que c’est?
C’est la faculté qu’ont certains systèmes déterministes simples d’évoluer de façon complexe.
Déterministes : relation stricte de cause à effet, pas de hasard
Simples : décrit par peu de variables
Bien que déterministes et simples, ces systèmes évoluent de façon non prédictible.
L’effet papillon
Le battement d’ailes d’un papillon à Lille provoque un ouragan en Martinique.
Cette image illustre la sensibilité aux conditions initiales, propriété à l’origine du chaos.
Dans un système chaotique, une petite différence dans l’état d’un système, par exemple dans la vitesse du vent et la température de l’air, est
amplifiée, et va mener, après un temps plus ou moins long, à deux situations complètement différentes. L’image que renvoie l’effet papillon est
La sensibilité aux conditions initiales entraîne la non-prédictibilité.
Pour prédire l’évolution d’un système chaotique, il faudrait connaître son état avec une précision infinie, ce qui est impossible. La précision de
notre connaissance de l’état initial détermine donc notre capacité à prédire l’avenir. Par exemple, plus nos données météos –température,
pression, vitesse du vent en chaque point du globe et à toutes les altitudes –sont nombreuses et précises, plus nos prévisions météos sont
précises. La quantité et la précision des données récoltées ne sont pas suffisantes : encore faut-il avoir un modèle capable de reproduire
fidèlement les mouvements de l’atmosphère, et des ordinateurs suffisamment puissants pour traiter toutes ces données et résoudre les
équations du modèle.
Quelques exemples
Prédateurs et proies
Variables
Le nombre de proies et de prédateurs
Paramètres
Le taux de naissance des proies
Le taux de mortalité naturelle des proies
Le taux de mortalité des prédateurs
Le taux de naissance des prédateurs
Interactions
Les prédateurs ne se reproduisent que s’ils
mangent suffisamment. S’ils tuent beaucoup de
proies, leur nombre augmente, mais le nombre
de proies diminue, et les prédateurs ont donc
moins de nourriture, et leur nombre décroit…Le
chaos apparaît dès qu’il y a trois espèces en
compétition (un couple proie-prédateur, et un
deuxième prédateur qui s’attaque aux deux
premières espèces).
L’atmosphère terrestre
Variables
La vitesse de déplacement de l’air et sa
température.
Paramètres
Les propriétés de viscosité de l’air
Les propriétés thermiques de l’air
La densité de l’air.
L’accélération de la pesanteur
Interactions
Une augmentation des écarts de température
entre deux lieux différents induisent une
augmentation du déplacement de l’air entre ces
deux lieux, qui diminue l’écart de température,
qui a tendance à ré-augmenter, par exemple
quand les deux lieux sont à des altitudes
différentes. C’est sur le modèle de Lorenz, une
version très simplifiée de la description des
convections de l’atmosphère terrestre, que le
chaos fut « découvert ».
Les lasers modulés
Variables
La quantité de lumière émise et le nombre
d‘atomes ou de molécules induisant cette
émission de lumière.
Paramètres
Les propriétés des atomes/molécules
L’énergie fournie au laser
La fréquence de la modulation
Interactions
Pour qu’un laser émette de la lumière, il faut
préparer les atomes (ou les molécules) dans un
état adéquat, en fournissant de l’énergie au
laser. Dès que le laser émet de la lumière, ce
nombre d’atomes diminue, la lumière émise
peut aussi diminuer. Si en plus on module
l’énergie fournie, du chaos peut apparaître.
Les lasers modulés sont à la base du fonction-
nement d’internet. Mais bien sûr, ceux qui sont
effectivementutilisés ne sont pas chaotiques!
incorrecte : il faudrait plutôt dire que, si le papillon ne bouge
pas, on aura un temps calme, alors que s’il bat des ailes, il
modifie localement la température de l’air et la vitesse du
vent, ce qui pourrait aboutir à une tempête plutôt qu’à un
temps calme. Ou l’inverse ! Bien sûr, en pratique, le
battement d’ailes d’un papillon n’est pas suffisant, car les
modifications qu’il induit ne dépassent pas quelques
centimètres. Il faut un évènement d’une autre ampleur;
comme une éruption volcanique par exemple.

L’ordre dans
Le chaos
www.physifolies.fr
L’espace des phases
Des attracteurs étranges
L’évolution dans le temps d’un système chaotique semble complètement désordonnée.
Pourtant, il y a bien un ordre caché dans le chaos déterministe.
Pour le trouver, il faut changer de point de vue.
Il ne faut plus regarder l’évolution des variables en fonction du temps, mais l’évolution des variables entre elles. Par exemple, dans le système
proies-prédateurs, on ne va plus regarder l’évolution du nombre de renards et du nombre de loups, mais on va tracer le nombre de loups en
fonction du nombre de renards. On dit qu’on ne regarde plus l’évolution du système dans le temps, mais dans l’espace des phases.
L’équilibre
Dans l’espace des phases, l’état du système est
un point. Ce point représente l’attracteur du
système : dans ce régime, quel que soit les
conditions initiales, on atteint l’équilibre entre les
renards et les loups, et la population reste
constante.
L’oscillation Le chaos
Quand le régime est chaotique, l’attracteur
n’occupe pas tout l’espace des phases, mais au
contraire il dessine une structure bien définie.
Cet attracteur possède des propriétés étranges.
Par exemple, il est fractal. On appelle ce type
d’attracteurs des attracteurs étranges.
Quand l’évolution temporelle est périodique,
l’attracteur est un cycle fermé.
Lorenz (météo) Lorenz 84 Polynôme de Sprott
RösslerPolynomial Polynomial