optique : travaux diriges n°1

L .PIETRI – Cours d’Optique – Première année PCSI
A - OPTIQUE
• Chapitre I : Lois générales de l’optique géométrique
• Chapitre II : Miroirs et lentilles sphériques dans l’approximation
de Gauss

L .PIETRI – Cours d’Optique – Première année PCSI
Chapitre I : Lois générales de l'optique géométrique
I – historique
I-1) Modèle Géométrique
I-2) Modèle Ondulatoire
I-3) Modèle Corpusculaire
II – Le rayon lumineux
II-1) Faisceau lumineux, notion de rayon lumineux
II-2) L’approximation de l’optique géométrique
II-2-1) L’onde électromagnétique
II-2-2) Longueur d’onde de la lumière
II-2-3) L’approximation de l’optique géométrique
II-3) Propagation de la lumière dans les milieux matériels
II-3-1) Absorption et dispersion
II-3-2) Propagation en milieu homogène et non homogène
II-3-3) Indépendance des rayons lumineux
III – Les Lois de Descartes
III-1) Réflexion et réfraction d’un milieu lumineux
III-2) Lois de Descartes
III-3) Réfraction
III-4) Principe de retour inverse de la lumière
IV – Construction géométrique de Huygens
IV-1) Le rayon réfléchi
IV-2) Le rayon réfracté
V – Réflexion totale
V-1) Réfraction limite (n1<n2)
V-2) Réflexion totale (n1>n2)
V-3) Applications
Chapitre I : Lois générales de l'optique géométrique

Introduction
L'optique est principalement l'ensemble des phénomènes perçus par l’œil. La cause de ces
phénomènes, la lumière, a été étudiée très tôt dans l'histoire des sciences, au point que tous les
principes peuvent sur lesquels reposent l’optique géométrique et l'optique ondulatoire sont connues
depuis le XIXème siècle.
Le but de ce chapitre va être dans un premier temps de voir sous quelles conditions les lois de
l'optique géométrique sont valables, ensuite nous poserons ces lois.
Mais dans un premier temps jetons un coup d’œil rapide sur l'historique de l'optique.
I – historique
I-1) Modèle Géométrique
Avant le XVIIème siècle, la nature de la lumière et sa propagation ne sont pas des questions
essentielles. Cependant des notions de rayons lumineux et de retour inverse de la lumière permette à
Euclide (300 ans av. J.-C.) de poser les bases de l'optique géométrique.
Il faut attendre le XIème siècle pour qu'Alhazen, physicien arabe attribue à la lumière une origine
extérieure à l’œil, définisse la notion d'images et interprète la formation des images dans l’œil.
Au XVIIème siècle, Descartes, Fermat et Newton donnent à l'optique géométrique sa véritable
grandeur ainsi Descartes énonce ces fameuses lois et propose un modèle corpusculaire, Fermat
propose une optique basée sur un principe de moindre action et Newton publie en 1704 « optics » où
ils présentent les lentilles, prismes et miroirs que nous verrons tout au long de ce cours.
I-2) Modèle Ondulatoire
Dès la fin du XVIIème siècle, Huygens suggéra une théorie ondulatoire de la lumière permettant
de retrouver les résultats de l'optique géométrique compatibles avec une vitesse de la lumière plus
grande dans l’air que dans les milieux matériels. La découverte, les siècles suivant des phénomènes
d'interférence de diffraction imposent cette théorie, suite aux travaux de Fresnel.
I-3) Modèle Corpusculaire
En 1906, Planck et Einsstein reviennent à un modèle corpusculaire en introduisant des quantas
d’énergie appelées photons : particules sans masse et d’énergie ε=hν déplaçant à la célérité de la
lumière.
Les deux modèles ondulatoires et corpusculaires, sont assez cohérents et se complètent.
Cette Dualité onde-corpuscule pour la lumière est alors généralisée aux particules dans la
théorie de la mécanique quantique par : De Broglie, Bohr, Heisenberg et Schrödinger.
Les quelques contradictions entre les deux modèles ont pu être levé par l’électrodynamique
quantique de Feynman, Schwinger et Tomonaga dans les années 50.
II – Le rayon lumineux
II-1) Faisceau lumineux, notion de rayon lumineux
Considérons une source lumineuse S de petites dimensions (par exemple un trou dans un
diaphragme éclairé par une lampe quartz-iode ; par définition la lumière issue de cette source
ponctuelle forme un faisceau lumineux.
Plaçons alors sur le trajet de ce faisceau un objet plan, l’ombre portée sur l’écran E et
homothétique de l’objet, quelquesoit la distance
de celui-ci à l’écran.
⇒ Le faisceau lumineux issu de S
est constitué de rayons lumineux rectilignes.
L .PIETRI – Cours d’Optique – Première année PCSI

Un laser fourni pratiquement en rayon lumineux : si l’on fait fonctionner laser dans l’obscurité,
on peut visualiser et le rayon lumineux. En fait si ce rayon évoque une droite, il a malgré tout de Dinant
une dimension transversale finit. On peut alors se demander s’il est aussi d’isoler rayon lumineux.
Pour se faire plaçons un diaphragme réglable à la sortie du laser ; si l’on retrécit trop l’ouverture
du diaphragme, la trace du faisceau sur un écran E donne une tâche qui s’élargit à la mesure que l’on
diminue a : ce phénomène porte le nom de diffraction. L’élargissement du faisceau laser, dans les
conditions que nous venons d’évoquer, se caractérise par un étalement angulaire ε dont l’expérience
permet d’écrire :
ε = λ /a où λ est une longueur caractéristique du rayon lumineux c’est à dire la longueur
d’onde.
⇒ on ne peut donc pas isoler un rayon lumineux. On peut cependant considérer qu’un faisceau
de lumière est formée de rayons lumineux, l’étude de la marche de ses rayons constituant le but de
l’optique géométrique.
⇒Le rayon lumineux est un modèle
II-2) L’approximation de l’optique géométrique
II-2-1) L’onde électromagnétique
Maxwell en 1873 a formulé les équations qui décrivent les ondes électromagnétiques…ainsi les
ondes électromagnétiques présente des similitudes avec les propagations des vibrations lors de la
chute d’un objet dans un liquide, vagues artificielles…
Les ondes électromagnétiques se propagent dans tout l’espace, même en l’absence de milieu
matériel avec une vitesse de propagation v et une fréquence f tel que :
λ=vT=v/f où λ est appelé longueur d’onde.
• λ = la période spatiale de l’onde (unité : mètre)
• T = la période temporelle de l’onde (unité : seconde)
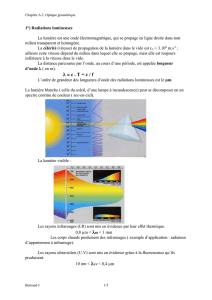
II-2-2) Longueur d’onde de la lumière
• La longueur d’onde de la lumière est définie par : λ=vT=v/ν où ν est la fréquence et v la
célérité dans le milieu considéré.
L .PIETRI – Cours d’Optique – Première année PCSI

Dans le vide : c = 299 792 458 ms-1.
• Le domaine visible de l’œil humain s’étend de 400nm (violet) à 750nm (rouge) avec une
sensibilité maximale dans le jaune vert à 560nm.
II-2-3) L’approximation de l’optique géométrique
L’approche géométrique constitue l'une bonne approximation des solutions des équations de
Maxwell tant que les caractéristiques géométriques du milieu varient peu à l'échelle de la longueur
d'onde. Dans le domaine visible, les dimensions étudiées sont bien supérieures à la longueur d'onde
du milieu ainsi l'optique géométrique est largement suffisante.
« L’étude vertu de l'optique géométrique suppose que les grandeurs caractéristiques du milieu
qui limitent les faisceaux ont des dimensions très supérieures à la longueur d'onde λ. »
II-3) Propagation de la lumière dans les milieux matériels
II-3-1) Absorption et dispersion
• Dans les milieux transparents la lumière se propage à la vitesse v=c/n où n est l’indice optique
du milieu qui dépend de la longueur d'onde, c’est la dispersion que l’on observera dans le prisme.
Pour les « verres » on peut utiliser la modélisation de Cauchy : n=A+B/λ2
• L'intensité lumineuse décroît lors de la propagation de la lumière dans le milieu matériel. La loi
de décroissance est en général une fonction exponentielle de la distance parcourue et dépend de la
fréquence, donc de la longueur d'onde : c'est le phénomène d’absorption.
II-3-2) Propagation en milieu homogène et non homogène
• Dans un milieu homogène et isotrope, la lumière se propage en ligne droite : les rayons
lumineux sont des droites.
• Par contre dans les milieux non homogènes c'est-à-dire présentant un indice variable, la
propagation de rayons lumineux n'est pas rectiligne.
• L'indice de la solution est une fonction croissante de la concentration en sucre dissout : cet
indice est donc plus important aux fond de la cuve. Il existe donc un gradient d’indice dirigé vers le bas
de la cuve. Nous observons une courbure des rayons lumineux dont la concavité, donc dans le sens
des indices croissants.
II-3-3) Indépendance des rayons lumineux
Nous supposerons dans la suite que le cheminement des différents rayons lumineux traversant
un instrument d'optique sont indépendants : c’est l’hypothèse de l'indépendance des rayons lumineux.
III – Les Lois de Descartes
III-1) Réflexion et réfraction d’un milieu lumineux
• Le plan défini par la normale et le rayon incident est par définition le plan d’incidence
L .PIETRI – Cours d’Optique – Première année PCSI