Enoncé UE515 Janv09

1
L3 GEEA - Option OH 8 Janvier 2009
FLSI 515 – Outils pour l’Ingénieur (P.Signoret + M. Myara) Durée: 2 h.
Aucun document autorisé – Calculatrice autorisée 3 pages
Etude de l’œil en optique paraxiale
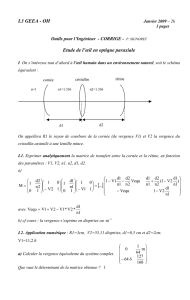
I On s’intéresse tout d’abord à l’œil humain dans un environnement naturel, soit le
schéma équivalent :
On appellera R1 le rayon de courbure de la cornée (de vergence V1) et V2 la vergence du
cristallin assimilé à une lentille mince. La rétine joue le rôle de récepteur, avec ses cellules
photosensibles.
I.1.
a) Exprimer analytiquement la matrice de transfert entre la cornée et la rétine, en fonction
des paramètres : V1, V2, n1, n2, d1, d2.
Montrer que la vergence équivalente s’écrit :
b) En écrivant une équation aux dimensions à partir de l’équation ci-dessus, déterminez (en le
justifiant) la dimension physique de la vergence Vequ dans le système MKSA.
I.2. Application numérique : R1=3cm, V2=55,11 dioptries, d1=0,5 cm et d2=2cm.
a) Calculer la vergence équivalente du système complet.
Que vaut le déterminant de la matrice obtenue ?
Vérifier numériquement que sous ces conditions l’œil considéré est emmétrope (formation
des images sur la rétine).
2
Rappels :
, où est la distance focale image équivalente du système optique épais, a le
coefficient M11 de la matrice de transfert et S le point axial de sortie du système complet.
La matrice de réfraction d’un dioptre sphérique, comme la matrice de transfert d’une lentille
mince, s’écrit : , où la vergence V vaut : pour un dioptre, et de
manière générale : .
Matrice de translation dans un milieu d’indice n :
Représenter sur papier millimétré à l’échelle x2 l’image d’un faisceau parallèle incliné par
rapport à l’axe optique. Vérifier ainsi le caractère emmétrope de l’œil.
Avec une autre couleur, tracer l’image d’un rayon quelconque parallèle à l’axe optique, et en
déduire le foyer image équivalent puis le plan principal image équivalent, que nous
désignerons respectivement Fi et Hi.
b) Sachant que V1,V2, d1 et n1 sont entachés d’une erreur de mesure de 3%, calculer
l’incertitude absolue sur la valeur de la vergence équivalente Vequ. Déduisez-en la valeur
numérique de l’incertitude relative sur Vequ.
c) Montrez que Vequ est une droite en fonction de V2, tous les autres paramètres étant
supposés constants. Calculez alors le coefficient directeur de cette droite ainsi que son
ordonnée à l’origine.
d) On a relevé expérimentalement Vequ en fonction de V2 pour plusieurs V2, avec une erreur
de mesure. On a obtenu le relevé ci-dessous :
Vequ
30
42
54
66
V2
36.60
50.98
62.69
71.55
Rappelez ce qu’est une droite de régression. Calculez ensuite le coefficient directeur et
l’ordonnée à l’origine de cette droite de régression.
Rappels : Le coefficient directeur de la droite de régression est donné par l’expression ci-
dessous, ainsi que l’erreur commise sur ce coefficient directeur.

3
Nota Bene : Dans tout ce qui suit, on ne demande aucune construction graphique.
II On s’intéresse à présent à l’œil en vision marine, par exemple immergé dans une piscine
(indice de réfraction : 1,33).
II.1. Quels sont les paramètres modifiés ?
II.2. L’eau rend-elle l’œil myope (focalise avant la rétine) ou hypermétrope (focalise après la
rétine) ?
III. Pour corriger cette vision aquatique, on utilise des lunettes de plongée.
III.1. On appelle z la distance entre ces lunettes et la cornée, f leur focale et ! l’épaisseur au
centre de ces lunettes.
Sans effectuer de calculs, trouver la configuration la plus simple (distance et focale) qui
permet de corriger la vision aquatique.
III.2. En notant la matrice de transfert établie au I.1, justifier analytiquement le
résultat trouvé intuitivement au III.1, en exprimant la matrice finale en fonction des
coefficients a, b, c, d et de z et !.
-----------------------------------------------