Examen 2009–2010 FMEE142 / Lasers

Examen 2009–2010
FMEE142 / Lasers
Deuxième session
•La calculatrice est autorisée
•Aucun document n’est autorisé
•Seule la communication avec le surveillant est autorisée
•Les différentes parties peuvent être traitées indépendamment.
Introduction
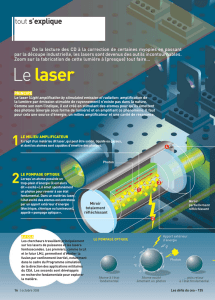
Nous étudions ici un laser à fibre optique dopée erbium (Er) émettant à la
longueur d’onde λ=1, 55 µm. Tel que représenté Fig. 1, la cavité laser
est constituée d’une fibre optique monomode dans laquelle deux miroirs
de Bragg réfléchissant autour de 1550 nm et séparés d’une distance dsont
photo-inscrits dans la fibre. Une fibre optique amplificatrice dopée Er est
soudée entre les deux miroirs. Cette fibre est pompée optiquement à 980 nm
grâce à une diode de pompe reliée à la cavité laser par un multiplexeur à
fibre optique.
d
Miroirs
de Bragg
Pompe optique
(980 nm)
Multiplexeur
980 nm
980 nm &
1550 nm1550 nm Fibre Er
Figure 1: Schéma de la cavité.
1

Examen M1 EEA FMEE142 / Lasers 2009–2010
1 Cavité passive
Du fait de la propagation dans la fibre optique monomode, il n’existe qu’un
seul mode tranverse. Nous notons r(R) le coefficient de réflexion en champ
(intensité) et t(T) le coefficient de transmission en champ (intensité) des
deux miroirs photo-inscrits du laser. Nous étudions la transmission par
la cavité d’un signal incident se propageant selon zet dont le champ élec-
trique est exprimé sous la forme d’une onde plane :
E=E0exp {i(k z −2π ν t)},
où k=2πn/λest la constante de propagation dans le milieu d’indice n,
ν=c/λla fréquence de l’onde, et cla vitesse de la lumière dans le vide.
1.1.- Déterminez la différence de marche entre deux ondes transmises
successivement à la sortie du Fabry-Perot en fonction de l’indice optique n
et de la longueur de cavité d.
1.2.- Déduire le déphasage φentre deux ondes transmises successive-
ment à la sortie de la cavité en fonction de l’indice optique n, de la longueur
de cavité d, et de la longueur d’onde λ.
1.3.- Déterminez le champ total transmis en sortie de la cavité. Montrez
que le champ transmis peut s’exprimer sous la forme :
E=E0t2exp(iφ/2)/1−r2exp(iφ)exp(−i2π ν t).
1.4.- Montrez que la transmission en intensité de la cavité peut s’exprimer
sous la forme d’une fonction d’Airy :
TFP =(1−R)2
(1−R)2+4Rsin2(φ/2). (1)
1.5.- Quelles sont les fréquences résonantes dans la cavité ?
Quelle est l’expression de l’intervalle spectral libre (ISL), différence de fréquence
entre deux fréquences résonantes successives ?
Donnez la valeur numérique de l’ISL pour n=1, 45 et d=1 m.
Donnez la valeur numérique de l’ISL pour n=1, 45 et d=0, 01 m.
1.6.- Les miroirs photo-inscrits sont typiquement des réseaux de Bragg.
Ces miroirs réfléchissent seulement dans une bande spectrale déterminée
(autour de la longueur d’onde de Bragg). Pour une largeur spectrale ∆λ=
0, 15 nm, déterminez combien de modes longitudinaux (environ) peuvent
exister pour les cavités de longueur 1 m et 0,01 m.
2

Examen M1 EEA FMEE142 / Lasers 2009–2010
2 Milieu amplificateur
Pour un pompage optique des ions erbium à 980 nm, le milieu amplifi-
cateur peut être assimilé à un système à trois niveaux d’énergie tels que
représentés Fig. 2.
Énergie
3
2
1
γ3
γlaser
WP
Figure 2: Système à 3 niveaux.
Les transitions ici considérées sont les suivantes :
•Les électrons sont pompés du niveau fondamental (1) vers le niveau
3 à un taux de transition WP(s−1),
•La durée de vie du niveau 3 est faible, et les électrons se désexcitent
rapidement vers le niveau 2 à un taux γ3=1/τ3(s−1),
•La transition laser correspond à la désexcitation du niveau 2 vers
le niveau 1 dont le taux de transition relativement lent est γlaser =
1/τlaser (s−1).
2.1.- Population électronique au niveau 3
2.1a.- Donner l’équation différentielle décrivant l’évolution temporelle
de la population électronique N3au niveau 3.
2.1b.- Déterminer la population électronique N3en régime stationnaire
en fonction de Wp,N1,τ3.
2.1c.- Sachant que WPτ31, montrer que la population N3en régime
stationnaire peut s’exprimer sous la forme :
N3≈Wpτ3N1.
3

Examen M1 EEA FMEE142 / Lasers 2009–2010
2.2.- Populations électroniques aux niveaux 1 et 2
2.2a.- Donner les équations différentielles décrivant l’évolution tem-
porelle des populations électroniques N1et N2aux niveaux 1 et 2 (respec-
tivement).
2.2b.- En étudiant l’équation sur la population N2en régime station-
naire, exprimer la population électronique N3en fonction de τlaser,τ3,N2.
2.3c.- En étudiant l’équation sur la population N1en régime station-
naire, déterminer la population électronique N2en fonction de τlaser,τ3,
WP,N1. Sachant que WPτ31, montrer :
N2≈WPτlaser N1.
2.3.- Inversion de population
2.3a.- Exprimez la population électronique totale Nen fonction de N2,
WP,τ3,τlaser.
2.3b.- Exprimez l’inversion de population ∆Npour la transition laser,
i.e., la différence N2−N1, en fonction de N2,WP,τlaser.
2.3c.- Montrer que l’inversion de population normalisée ∆N/Npeut
s’exprimer sous la forme suivante :
∆N
N≈τlaser WP−1 τlaser WP+1.
2.3d.- À quelle condition obtenons-nous du gain ?
2.3e.- Tracez l’évolution de cette inversion de population en fonction du
taux de pompage WPet commentez.
4

Examen M1 EEA FMEE142 / Lasers 2009–2010
3 Cavité active
Nous étudions ici une cavité courte fonctionnant sur un seul mode longi-
tudinal, et prendrons par la suite d=0, 01 m. Soient Lles pertes linéiques
équivalentes cumulées sur un aller-retour dans la cavité laser (pertes des
miroirs et pertes de propagation). Nous rappelons l’expression en intensité
du gain linéique :
G=G0
(1+Y),
où G0est le gain petit signal et Yl’intensité laser normalisée à l’intensité de
saturation. Rappelons que G0est proportionnel à l’inversion de population
∆N, qui croît avec le taux de pompage WP.
3.1.- Quelle condition sur le gain doit être vérifiée pour obtenir l’effet
laser ?
3.2.- En appliquant cette condition, montrez que l’intensité laser nor-
malisée peut s’exprimer sous la forme :
Y=G0
L−1.
3.3.- Pour quelle valeur du gain petit signal G0le seuil laser est-il at-
teint ?
3.4.- Tracez l’allure de l’évolution de la puissance optique avec le taux
de pompage pour deux valeurs de pertes et commentez.
5