document - Université de Rennes 1

Introduction
Le principe de l’IRM
Quelques applications
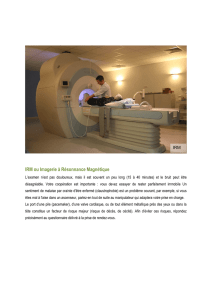
L’Imagerie par Résonance Magnétique
nucléaire
Problèmes mathématiques et numériques
G. Caloz, P. Boissoles 1S. Balac 2
1IRMAR, UMR 6625
Université de Rennes 1
2Centre de Mathématiques
INSA de Lyon
23 juin 2005 / Séminaire d’analyse numérique, Nantes
Problèmes issus de l’IRM

Introduction
Le principe de l’IRM
Quelques applications
Plan de l’exposé
1Introduction
Présentation générale
Pour la petite histoire
2Le principe de l’IRM
La RMN
La localisation du signal - les gradients
3Quelques applications
Effet d’un champ magnétique additionnel
Problèmes de la magnétostatique
Phénomènes d’échauffement
Problèmes issus de l’IRM

Introduction
Le principe de l’IRM
Quelques applications
Présentation générale
Pour la petite histoire
Collaboration
C’est une collaboration avec le LRMBM (Laboratoire de
Résonance Magnétique en Biologie et Médecine) de
l’Université de Rennes 1 : J.D. De Certaines, G. Cathelineau,
H. Boukhil,...
Comment interpréter les images obtenues par les imageurs ?
Modélisation du processus de construction des images
Algorithmes de construction
Construction numérique des images pour y insérer de
l’information
Problèmes issus de l’IRM

Introduction
Le principe de l’IRM
Quelques applications
Présentation générale
Pour la petite histoire
Un premier problème
FIG.: Une sphère : image expérimentale (gauche) et image calculée
(droite)
Problèmes issus de l’IRM

Introduction
Le principe de l’IRM
Quelques applications
Présentation générale
Pour la petite histoire
Des champs magnétiques à étudier !
FIG.: Imageur
Problèmes issus de l’IRM