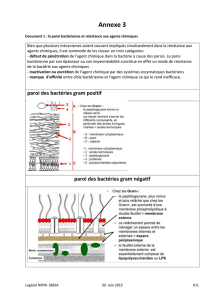
Modèles de champ de phase de type Cahn

Modèles de champ de phase de type Cahn-Hilliard:
modélisation et conditions aux limites
Alain Miranville
Université de Poitiers

L’équation de Cahn-Hilliard
Proposée à la fin des années 1950 (J.W. Cahn et J.E. Hilliard)
Très importante en science des matériaux : décrit les processus de séparation
de phase dans des alliages métalliques binaires (exemple : Aluminium/Zinc)
Nucléation partielle
Nucléation totale : décomposition spinodale
Coalescence
Importants pour les propriétés mécaniques ou le vieillissement

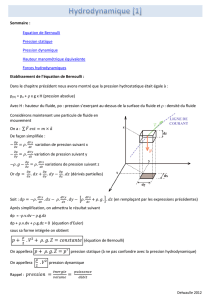
Equation de Cahn-Hilliard :
∂u
∂t+κα∆2u−κ∆f(u) = 0
•u: paramètre d’ordre (densité d’atomes)
Composants A et B : u=uAet uB=1−uA(uA+uB=1)
•κ: mobilité (constante strictement positive)
•α > 0 : liée à la tension surfacique à l’interface
Remarques :
a) On peut écrire l’équation sous la forme
∂u
∂t+κ∆2u−κ ∆f(u) = 0
 > 0 : liée à l’épaisseur de l’interface

b) Modèle à interface diffuse :
L’interface est d’épaisseur non nulle
Le paramètre d’ordre varie continument entre 0 et 1
Modèles de champ de phase : à comparer aux modèles à interface raide
(exemple : modèle de Stefan)
c) En géneral, on fait un changement d’échelle : u→2u−1
2
uprend ses valeurs entre −1 et 1
−1 et 1 : états purs

•f: dérivée d’un potentiel à 2 puits F
Choix usuel :
F(s) = 1
4(s2−1)2,f(s) = s3−s
Approximation de potentiels logarithmiques (obtenus à partir d’un modèle de
champ moyen) :
F(s) = −θ0s2+θ1((1+s)ln(1+s)+(1−s)ln(1−s))
s∈(−1,1),0< θ1< θ0
f(s) = −2θ0s+θ1ln 1+s
1−s,s∈(−1,1)
Termes logarithmiques : liés à l’entropie de mélange