1 Graphe orienté valué 2 Implémentation

Université Claude Bernard - Lyon 1 Licence Sciences et Technologies - L3
Algorithmique, Programmation et Complexité - LIF9 Semestre de printemps
TP - Graphes orientés, algorithme de Dijkstra
1 Graphe orienté valué
Le but est de développer une structure générique de graphe et d’implémenter l’algorithme de Dijkstra
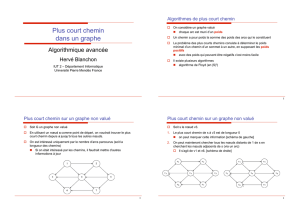
pour la recherche de plus courts chemins. Nous allons considérer des graphes orientés et valués :
Truc
Chose
Machin Bitoniau
Bidule
8
2
7
45
1
3
12
7
10
Les valuations des arcs seront des entiers. Chaque nœud devra posséder, entre autres, une chaîne de
caractère correspondant par exemple à un nom de ville. Dans les fonctions et procédures à implémenter,
l’accès à un nœud se fera par l’intermédiaire de cette chaîne de caractère. Le graphe devra être représenté
à l’aide de listes d’adjacence (pas de matrice !), avec un accès optimisé aux arcs incidents extérieurement
à un nœud donné.
2 Implémentation
Comme pour les TPs précédents, vous avez le choix entre le passage de paramètre par pointeur ou
par référence. Chaque procédure/fonction développée devra être testée dans le programme principal.
Les procédures/fonctions demandées peuvent faire appel à d’autres procédures/fonctions internes de
votre choix. Votre code devra comporter :
1) La définition des structures Graphe,Noeud et Arc. Les collections d’éléments, quels que soient leurs
types, devront être implantées de manière à éviter le déménagement en mémoire des éléments en cas
d’insertion ou de suppression.
2) Une procédure d’initialisation d’un graphe vide
procédure initGrapheVide(donnée-résultat G : Graphe)
3) Une fonction d’ajout d’un nœud avec un nom donné
fonction ajoutGrapheNoeud(donnée-résultat G : Graphe, donnée nom : chaîne) : entier
Si un nœud portant le même nom est déjà présent dans le graphe, la fonction ne modifie pas celui-ci. La
valeur de retour pourra être utilisée pour indiquer si l’ajout du nœud a eu lieu ou non.
4) Des fonctions d’ajout d’un arc de valeur ventre deux nœuds identifiés par leur noms respectifs.
fonction ajoutGrapheArc(donnée-résultat G : Graphe, donnée v : entier,
donnée nom_départ : chaîne, donnée nom_arrivée : chaîne) : entier
Si au moins un des deux nœuds n’existe pas, la fonction ne modifie pas celui-ci. Si un arc existe déjà entre
les deux nœuds , l’ancienne valeur de cet arc est remplacée par v. La valeur de retour pourra être utilisée
pour indiquer si l’arc a été ajouté, modifié ou ignoré (si les sommets passés spécifiés ne sont pas valides).
5) Une procédure de destruction complète d’un graphe (destinée à être appelée en fin de programme)
procédure detruitGraphe(donnée-résultat G : Graphe)
1

6) Une procédure d’affichage en mode texte
procédure afficheGraphe(donnée G : Graphe)
La procédure devra afficher pour chaque nœud , au moins l’ensemble des successeurs et le coût des arcs
correspondants.
7) Une procédure implémentant l’algorithme de Dijkstra vu en cours. Le nom du nœud de départ ssera
passé en paramètre :
procédure Dijkstra(donnée-résultat G : Graphe, donnée s : chaîne)
La procédure devra afficher le plus court chemin (et la longueur de ce chemin) du nœud sà tous les
autres nœuds . Une implémentation digne de ce nom devra utiliser une structure de donnée optimisée
pour retrouver rapidement, à chaque itération, le nœud le plus proche (en terme de distance parcourue).
8) Des fonctions de suppression d’un arc, identifié par les noms des nœuds de départ et d’arrivée
fonction supprimeGrapheArc(donnée-résultat G : Graphe,
donnée nom_départ : chaîne, donnée nom_arrivée : chaîne) : entier
La valeur de retour pourra être utilisée pour indiquer si la supression de l’arc a eu lieu ou non.
9) Des fonctions de suppression d’un nœud ,
fonction supprimeGrapheNoeud(donnée-résultat G : Graphe,
donnée nom : chaîne) : entier
La valeur de retour pourra être utilisée pour indiquer si la supression du nœud a eu lieu ou non. La sup-
pression d’un nœud doit entraîner la suppression de tous les arcs qui lui sont incidents intérieurement
ou extérieurement.
3 Conditions de rendu
A la date de rendu, vous devrez déposer une archive (formats valables : tar.gz, tgz ou zip) au nom
du ou des étudiant(s) (ex : DUPONT.zip ou DUPONT_DURAND.tar.gz) sur SPIRAL. Le nom du dépôt
et la date limite vous seront communiqués ultérieurement.
Cette archive devra contenir tous les fichiers .c et .h, ainsi que le fichier Makefile. Attention :
— Votre archive NE DOIT PAS contenir de fichiers objets (.o) ni d’exécutable.
— Vérifiez la validité de l’archive en pièce jointe sur le message envoyé.
— Toute récupération flagrante du code d’autrui sera sanctionnée.
— Votre programme doit pouvoir être compilé sans erreur ni avertissement avec g++ ou gcc, sui-
vant que vous utilisez la notion de référence ou non (à préciser dans le Makefile), et avec les
options de compilation -Wall -ansi -pedantic
— L’interface de vos modules doit offrir toutes les informations utiles à l’utilisation des types et des
fonctionnalités offertes.
— L’exécution ne doit pas générer de fuite mémoire. Utilisez valgrind pour vérifier que toute la
mémoire allouée est correctement libérée.
2