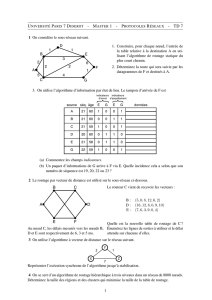
Travaux Dirigés Couche 3

Université Paris 1
Panthéon Sorbonne
Master 1 MIAGE
Réseaux
2013/2014
Travaux Dirigés
Couche 3 - Routage
Exercice 1
1˚) Les réseaux de datagrammes routent chaque paquet individuellement, ce que ne font pas les réseaux à circuit
virtuel. Est-ce que cela signifie que les routeurs des réseaux à circuits virtuels n’ont pas la capacité à router des
paquets isolés ?
Exercice 2 (Routage Dynamique)
1˚) Rappeler la motivation et le principe du routage dynamique. En quoi est-il distribué ?
2˚) Rappeler le principe du routage par vecteur de distance et du routage par état des liens.
Exercice 3 (Stabilisation des tables de routage)
On utilise l’algorithme à vecteur de distance sur le réseau suivant.
Représenter l’exécution synchrone de l’algorithme jusqu’à stabilisation.
Exercice 4 (Vecteur de distance)
Le routage par vecteur de distance est utilisé sur le sous-réseau ci-dessous.
Au noeud C, les délais mesurés vers les noeuds B, D et E sont respectivement de 6, 3 et 5 ms.
Le routeur C vient de recevoir les vecteurs :
— B : (5 ; 0 ; 8 ; 12 ; 6 ; 2)
— D : (16 ; 12 ; 6 ; 0 ; 9 ; 10)
— E : (7 ; 6 ; 3 ; 9 ; 0 ; 4)
1˚) Quelle est la nouvelle table de routage de C ?

Master 1 MIAGE Réseaux
Exercice 5
Hypothèses pour les prochaines questions :
1. Toutes les liaisons ont un coût égal à 1 sauf la liaison numéro C-D qui a un coût de 8.
2. On s’intéresse uniquement aux chemins vers D, et on suppose qu’après initialisation, les tables de routage
ont la valeur suivante :
Vers D Passerelle Coût
A B 2
B D 1
C B 2
3. Nous considérons que la liaison numéro B-D tombe en panne.
Rappel : une table émise par un noeud X, peut atteindre les noeuds voisins Yet Zdans des délais différents.
NB : dans la suite de l’exercice, pour chaque étape des scénarii d’évolution des tables, vous préciserez bien
quels sont les échanges de tables, i.e. le noeud qui a émis une table et celui (ou ceux) qui la reçoi(ven)t.
Utilisation des vecteurs de distance sans optimisation
1˚) Comment la rupture de la liaison numéro B-D est-elle détectée ? Donnez la valeur des tables de routage juste
après cette détection.
2˚) Donnez un scénario d’évolution des tables jusqu’à leur stabilisation, dans le cas le plus favorable.
3˚) Que se passe-t-il si, après l’envoi de la nouvelle table de B(que Ba envoyée après détection de la rupture),
Breçoit l’ancienne table de A(que Aa envoyée avant détection de la rupture) ? Montrer l’évolution des tables
jusqu’à leur stabilisation, dans un des scénarii les plus défavorables.
Utilisation des vecteurs de distance avec horizon partagé
4˚) Rappeler brièvement le principe de cette technique.
5˚) Pourquoi la technique de l’horizon partagé ne permet-elle pas de maîtriser le problème des boucles dans le
cas précédent ? Conclusion ?
2013/2014 – Travaux Dirigés page 2/5

Master 1 MIAGE Réseaux
Exercice 6 (Routage par vecteur distance)
Un inter-réseau est constitué de réseaux locaux Li et de routeurs Gi. Le tableau suivant indique les liaisons
entre les réseaux et les routeurs.
— G1 reliée à L1 (192.168.1.0/24), L3 (192.168.3.0/24) et L4 (192.168.4.0/24)
— G2 reliée à L1 et L2 (192.168.2.0/24)
— G3 reliée à L4 et L5 (192.168.5.0/24)
— G4 reliée à L2 et L5
1˚) Faire un schéma du réseau
2˚) Indiquer l’évolution des tables de routage de chaque routeur. Le coût est calculé en nombre de sauts ; il
est nul si le réseau est directement accessible. En cas d’égalité de coût, le chemin vers le routeur de plus petit
identificateur sera choisi.
3˚) Au bout de combien d’itérations le procédé converge-t-il ?
4˚) Comment évoluent les tables si G3 tombe en panne ?
Exercice 7 (Routage distribué (routage par le vecteur distance Bellman-Ford))
On considère la topologie du réseau suivant :
Considérons le noeud J. Il reçoit les tables de routage de ses voisins immédiats A, I, H et K, représentées
dans les tableaux ci-dessous. De même, la distance mesurée entre J et chaque voisin est indiquée en bas de
chaque tableau.
1˚) Déterminer la nouvelle table de routage de J.
2013/2014 – Travaux Dirigés page 3/5

Master 1 MIAGE Réseaux
Exercice 8
Établissez la table de routage du noeud E de ce réseau, en minimisant le coût des liaisons. Vous supposerez que
la topologie entière du réseau est connue.
1˚) Vous utilisez un algorithme à vecteurs de distance.
2˚) Vous utilisez un algorithme à état des liens.
209
Le routage
8
Chapitre
Problèmes et exercices
EXERCICE 1 TABLE DE ROUTAGE
La table de routage du nœud E peut être, par exemple :
routage(E) = [(A, B) ; (B, B) ; (C, B) ; (D, D) ; (E, –) ; (F, F)] où le couple (A, B) signifie :
pour aller à A, il faut passer par B.
Il y a deux chemins de longueur 2 pour aller de E à A, celui qui passe par B et celui qui
passe par F. Nous avons retenu celui qui correspondant à la plus petite lettre dans l’ordre
alphabétique. De même pour le chemin de E à C.
Avec un algorithme à état des liens, il faut comparer les différents chemins. Le chemin E-B-A
est de coût 7 + 2 = 9 alors que E-F-A est de coût 3 + 4 = 7. Ce dernier est meilleur.
Remarquons qu’un chemin long comme E-F-D est meilleur que le chemin direct E-D
puisque 3 + 3 = 6 est meilleur que 7. L’algorithme de Dijkstra doit donc explorer tous
les chemins.
On procède par étapes. Cherchons les chemins de longueur 1. On trouve E-B = 2, E-D = 7,
E-F = 3. Cherchons maintenant les chemins plus longs à partir du lien le plus prometteur,
c’est-à-dire E-B. On trouve E-B-A = 2 + 7 = 9 et E-B-C = 2 + 5 = 7. Cherchons ensuite les
chemins plus longs à partir du lien prometteur suivant c’est-à-dire E-F. On trouve E-F-
A = 3 + 4 = 7, meilleur que l’information précédemment calculée : cette dernière est effa-
cée, on ne conserve que le meilleur chemin. De même E-F-D = 3 + 3 = 6 est meilleur que
E-D précédemment calculé à 7. On continue ainsi en explorant les chemins à partir du
lien prometteur suivant, ici E-C, etc.
La table de routage de E est finalement :
routage(E) = [(A, F) ; (B, B) ; (C, B) ; (D, F) ; (E, –) ; (F, F)].
Établissez la table de routage du nœud E de ce réseau, en minimisant le coût des
liaisons. Vous supposerez que la topologie entière du réseau est connue.
Vous utilisez un algorithme à vecteurs de distance.
Vo us u t il i se z u n a lg o r it h me à é t at d e s l ie n s q ui s ’a ppu i e s ur la mé t r iq u e i nd i qu ée à l a
figure 8.5.
Figure 8.5
Topologie et
métrique du
réseau.
A
B
E
C
D
F
4
7
2
3
3
5
3
7
Exercice 9 (Dijkstra)
On considère le sous-réseau suivant :
1˚) Construire, pour chaque noeud, l’entrée de la table relative à la destination A en utilisant le routage dyna-
mique du plus court chemin.
2˚) Déterminez la route que sera suivie par les datagrammes de F destinés à A.
3˚) Énoncez un pseudo-algorithme qui permet la détermination du chemin le plus court dans un graphe (algo-
rithme de Dijkstra).
2013/2014 – Travaux Dirigés page 4/5

Master 1 MIAGE Réseaux
Exercice 10
Les coûts entre les noeuds peuvent être fonction de la distance, de la longueur moyenne des files d’attente, du
débit des liaisons, du coût des liaisons, etc... Déterminer le plus court chemin (algorithm de Dijkstra) entre le
noeud A et le noeud D de la figure 10 pour les métriques suivantes :
— distance physique
— débit moyen
— RTT
— coût
Figure 1 – Réseau
Exercice 11 (Broadcast)
1˚) En partant du sous-réseau de la figure ci-dessous, combien de paquets sont générés par une diffusion broadcast
initiée par B, au moyen de :
— l’algorithme RPF ?
— l’arbre couvrant SPF ?
5On considère le sous-réseau suivant et un arbre collecteur sous-jacent enraciné en B.
B
A
F
DEC
J
N
O
I
H
G
L
M
K
1. Combien de paquets sont générés par une
diffusion broadcast initiée par B utilisant
(a) l’arbre collecteur ?
(b) l’algorithme RPF (Reverse Path For-
warding) ?
2. Imaginons qu’une nouvelle ligne soit ajou-
tée entre Fet G, mais que l’arbre collec-
teur ne change pas. Quelles modifications
cela entraîne-t-il ?
6On considère le réseau ad hoc suivant.
1. Rappelez le principe de l’algo-
rithme AODV (Ad hoc On-demand Dis-
tance Vector). Quel est le format des pa-
quets ROUTE REQUEST et ROUTE REPLY.
2. Décrivez le comportement de cet algo-
rithme dans le cas où un processus du
nœud A cherche à envoyer un paquet au
nœud I.
3. Proposez une table de routage possible
pour le nœud D et précisez les voisins ac-
tifs pour chaque destination. Quelle serait
la réaction de D s’il apprenait que G ne fait
plus partie du réseau ?
C
B
A
D
E
G
IH
F
4. Supposons que le nœud B vienne juste de
redémarrer et que sa table de routage soit
vide. Il a subitement besoin d’une route
vers H. Il envoie des paquets broadcast
avec des valeurs de durée de vie de 1, 2,
3, etc. Combien de cycles de diffusion re-
quiert la découverte d’une route ?
7On considère le réseau ci-dessous. Les hôtes dont le nom termine par aforme un groupe multicast.
A
B
C
D
EF
G
3
2
4
4
1
1
2
4
bravo
tango
charlie
alphaechodelta
india
november
oscar
papa
quebec
uniform
victor
zanzibar
lima
2
3
1. Déterminez les chemins unicast de papa vers chacun des autres membres du groupe.
2. Déterminez un arbre multicast enraciné en papa. Est-il de coût minimal ?
3. Décrivez les changements produits par les arrivées successives de tango et de zanzibar dans le
groupe.
4. Décrivez les changements produits par les départs successifs d’india et de lima du groupe.
2
2013/2014 – Travaux Dirigés page 5/5