1 . Montage On alimente une résistance R sous une

OHM Georg Physicien allemand 1789 1854
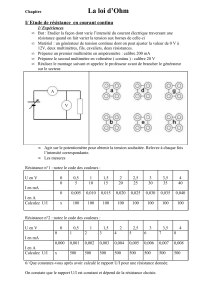
1 . Montage
On alimente une résistance R sous une tension variable .
On mesure l'intensité du courant dans la résistance avec .
On mesure la tension sur R avec .
Résultats : Pour une résistance de 15 ohms environ on obtient le tableau suivant :
i(mA) U (V) U / i avec U en V et i en A
50 0,73 14,6 Moyenne 14,5 voisin de 15
100 1,46 14,6 On observe donc que le rapport U / i est constant et égal
125 1,80 14,4 à R . On admettra que cela est toujours vrai pour une
150 2,16 14,4 résistance
175 2,51 14,3 .
U
i
=R
ou ( 1 )
U et i sont proportionnels . Le coefficient de proportionnalité est R .
Représentation graphique
Dans la formule (2) ci-dessus divisons par i des 2 côtés du signe = . On obtient
U / i = ( R*i ) / i Simplifions par i à droite , il reste ( 3 )
Loi d'Ohm : Une résistance R parcourue par un courant i présente à ses bornes
une tension U telle que ( avec U en Volts , R en Ohms et i en Ampères )
Pour retenir : cacher R , il reste U / i ; écrire la formule
cacher i , il reste U / R ; écrire la formule
LOI d'OHM
A
V
Potentiomètre
La représentation de U en fonction de i est
une droite . Cette droite est appelée la
caractéristique de la résistance .
( U / i ) * i = R * i
Simplifions par i à gauche . On obtient :
Dans la formule (1) ci-dessus multiplions
par i des 2 côtés du signe =
U = R * i ( 2 )
U / i = R
U = R * i
U
R i
U / i = R

2 . Exercices sur la loi d'Ohm
On donne : Calculer :
1 ) R = 500 Ω i = 0,2 A U
2 ) R = 2 kΩ i = 0,5 A U
3 ) R = 200 Ω i = 20 mA U
4 ) U = 10 V R = 2 Ω i Attention aux unités : A , V , Ω
5 ) U = 0,2 V R = 100 Ω i
6 ) U = 15 mV R = 3 Ω i
7 ) U = 150 V i= 4 A R
8 ) U = 20 mV i = 0,2 A R
9 ) U = 4 V i = 50 mA R
Les réponses sont données dans le désordre :
7) 37,5 Ω 1) 100 V 9 ) 80 Ω 2 ) 1 000 V 5 ) 2 mA 4 ) 5 A 8 ) 0,1Ω 6 ) 5 mA 3) 4 V
3 . Thermistances
La caractéristique du résistor étudié au 1 est une droite passant par l'origine On dit que ce résistor
est linéaire . La résistance ne change pas lorsque l'intensité varie .
Par contre si l'on étudie une petite lampe à incandescence avec le même montage , la caractéristique
est une ligne courbe : il n'y a plus proportionnalité entre i et U : le quotient de U par i qui donne la
résistance augmente progressivement pendant que l'ampoule brille de plus en plus et que son
filament est de plus en plus chaud : R passe de 1,5 ohm à froid à 15 ohms à la température maxi .
La lampe n'est pas un composant linéaire à cause de la variation de sa température.
Le résistor utilisé au 1 ne chauffait pas car l'intensité était modérée .
un relevé en page 3
Il existe des résistances
spécialement utilisées pour
leur variation de résistance
en fonctionde la
température . Elles ne
suivent pas la loi d'Ohm :ce
sont les thermistances
1er type : les thermistances à coefficient de températu
re négatif ( CTN )
Leur résistance diminue lorsque leur température augmente
Leur température varie en fonction du passage du courant
et (ou) de la température ambiante .
Utilisation :
Mesure de température
régulation de température , capteur pour thermostat
dérive thermique des transistors
temporisation , protection contre les surintensités
i i
U
R

2eme type : les thermistances à coefficient de températu
re positif ( CTP )
Leur résistance augmente avec la température : partie 2 de
la courbe ci-contre
Leur température varie en fonction du passage du courant
et (ou) de la température ambiante .
Utilisation :
protection des transistors contre les amballements
thermiques
protection des moteurs électriques contre les surchauffes
stabilisation du courant des lignes téléphoniques
Relevé intensité - tension pour une ampoule de lampe de poche
I (mA)
0
120
150
200
250
300
U (V)
0
0,41
0,77
1,33
2,04
2,94