LA SANTÉ

LA SANTÉ
Chapitre IV : Concentration et
quantité de matière
I- Mole et concentration molaire
Une mole d’entités est un paquet contenant 6,02.10^(23) entités.
La quantité de matière d’une espèce chimique représente
le nombre de moles (de paquets) contenues dans un
échantillon de cette espèce. On la note net on l'exprime en
mole de symbole mol.
On a : n = N / NA avec :
n: quantité de matière (mol)
N: nombre d'entités (sans unité)
NA: constante d'Avogadro NA = 6,02.10^(23) mol^(-1)
La concentration molaire est la quantité de matière de
soluté dissoute divisée par le volume de la solution
C = n/V soit n = C x V avec:
C: Concentration molaire (mol/L)
n: quantité de matière ou nombre de mol (mol)
V: Volume (L)
Il existe aussi la concentration massique Cm = m/V d’autre part
C = Cm/M soit C = m/ (M*V) avec:
Cm: concentration massique (g/L)
m: masse (g)
M: masse molaire (g/L)
II- Détermination d'une quantité de matière
La masse molaire atomique M d’un élément est la masse d’une
mole de cet élément, son unité est le g/mol
Les valeurs des masses molaires atomiques des différents éléments
se trouvent dans la classification périodique des éléments
Exemple : M(H) = 1 g.mol/L ; M(C ) = 12 g/mol ; M(0) = 16 g/mol
La masse molaire moléculaire M d’une espèce est la masse
d’une mole de molécule de cette espèce chimique. Elle
s’exprime en g/mol
On calcule une masse molaire moléculaire en effectuant la
somme des masses molaire atomiques de tous les atomes
constituants la molécule.
Détermination de la quantité de matière:
m = n x M ou n = m/M avec:
m: masse (g)
n: quantité de matière ou nbre de mol (mol)
M: masse molaire (g/mol)
Parfois nous n’avons pas accès directement à la masse de
l’échantillon, mais à sa masse volumique ,un petit calcul
intermédiaire est alors nécessaire.
On définit la masse volumique  =m/V soit m= x V
On obtient donc n =  x V / M
III- Préparation d'une solution
Lors d’ une dissolution une quantité
donnée d’espèce chimique solide est
dissoute dans un volume donné de
solvant. Pour obtenir une
concentration précise on utilise lors
de la dissolution une fiole jaugée
Diluer une solution c’est diminuer sa concentration par
ajout de solvant.
n solution mère prélevée = n solution fille préparée
C0 . V0 = C1 . V1
Chapitre V : Préparation
d'un médicament
I- Évolution d'un système chimique
Un système chimique est un ensemble
d’espèces chimiques.
L’état d’un système chimique est décrit à
un instant donné en indiquant :
-La nature (la formule) de l’espèce
chimique, ainsi que son état physique.
-Les quantités de matière présentes.
- La température et la pression
L’état initial est l’état du système à
l’instant de la mise en contact des espèces
chimiques du système.
L’état final est l’état du système lorsque
celui-ci a fini d’évoluer, c'est-à-dire lorsque
les quantités de matière de chaque
constituant du système est constant.
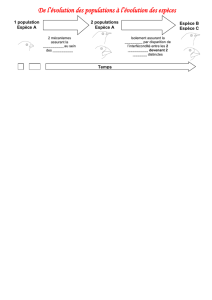
Un réactif est une espèce chimique qui a sa
quantité de matière qui diminue ( elle peut
s’annuler) entre l’état initial et l’état final.
Un produit est une espèce chimique dont la
quantité de matière augmente entre l’état
initial et l’état final.
-Si le système libère de l’énergie, la
réaction est dite exothermique , dans ce cas
on a une élévation de la température (voir
une mise en mouvement, l’apparition de
lumière, ou une circulation d’électrons et
donc d’un courant en électricité)
-Si le système absorbe de l’énergie, la
réaction est dite endothermique , dans ce cas
on a une diminution de la température
II- Équation d'une réaction chimique
Une réaction chimique est décrite par une équation
de la réaction chimique . Son écriture est telle que :
-La formule brut et l’état physique des réactifs, sont
placés à gauche de la flèche symbolisant l’évolution
du système.
-La formule brut et l’état physique des produits,
sont placés à droite de la flèche symbolisant
l’évolution du système
Méthode pour ajuster les coefficients
stoechiométriques:
a) Identifier les réactifs et les produits en précisant leur
état physique.
b) Ecrire la formule brut des différents constituants à
gauche (les réactifs) et à droite (les produits) de la
flèche symbolisant l’évolution du système.
c) Compter le nombre d’éléments de part et d’autre de
la flèche.
-S’il y a le même nombre d’éléments des deux côtés
pour tous les éléments présents, alors les coefficients
stœchiométriques sont ajustés. La loi de conservation
des éléments est ainsi vérifiée.
-Sinon, faire précéder la formule brut du coefficient
stœchiométrique permettant d’assurer la conservation
des éléments.
d) Réécrire l’équation de la réaction avec les coefficients
stœchiométriques ajustés, puis vérifier la loi de
conservation des charges.
Toutes les lois de conservation sont alors respectées :
conservation de la matière et des charges.
Chapitre III : Les
molécules
Les atomes n’existent que très
rarement sous forme isolée.
Spontanément ils s’assemblent entre
eux pour former des molécules.
Une liaison assemble deux atomes A
et B d’une même molécule. Elle est
symbolisée par un tiret : A-B.
Cette liaison est appelée liaison
covalente, elle correspond à la mise
en commun de deux électrons par
deux atomes, chaque atome
fournissant un électron
Les différents types de formules
(a) Formule brute : elle indique la
nature et le nombre des atomes
présents dans le composé.
(b) Formule développée : elle fait
apparaître tous les atomes et toutes
les liaisons entre les atomes du
composé. Les angles entre les liaisons
pour cette représentation sont en
général de 90° (ou de 120° dans
certains cas)
(c) Formule semi-développée : elle
fait apparaître tous les atomes et
toutes les liaisons entre ces atomes à
l’exception des liaisons avec les
atomes d’hydrogène
a) Comment représenter une molécule ?
Pour représenter une molécule il faut:
1- Faire la liste de tous les atomes qui
interviennent dans la molécule.
2- Ecrire la structure électronique de
chaque atome.
3- Déterminer le nombre d’électrons
externes pour chaque atome.
4- Trouver le nombre de liaisons
covalentes que chaque atome doit établir
pour satisfaire la règle de l’octet (ou du
duet), ce qui correspond au nombre
d’électrons que chaque atome doit
acquérir.
5- Représenter la molécule de manière à
ce que chaque atome établisse le bon
nombre de liaisons covalentes.
Chapitre II : Composition d'un
médicament
III- Extraction et
séparation d'une espèce
chimique
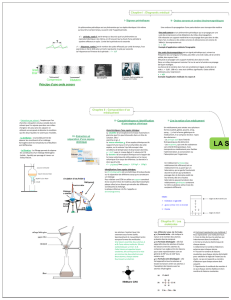
-Extraction par solvant :l’espèce que l’on
cherche à récupérer est plus soluble dans le
solvant que l’on ajoute que dans son milieu
d’origine. On peut ainsi les séparer en
utilisant une ampoule à décanter à condition
que les deux liquides ne soient pas miscibles.
-La distillation : ce procédé permet de
séparer les constituants d’un mélange
homogène dont les températures d’ébullition
sont différentes
-La filtration : Le filtrage permet de séparer
les constituants d’un mélange hétérogène
(solide - liquide) par passage à travers un
milieu filtrant.
II- Caractéristiques et identification
d'une espèce chimique
Caractéristiques d'une espèce chimique
La solubilité d’une espèce est la masse maximale en
gramme que l’on peut dissoudre dans un litre de
solution. Elle s’
exprime en g.L-1
La masse volumique d’une espèce chimique est le
rapport d’une masse m d’un échantillon de cette
espèce, sur le volume V qu’elle occupe à des
conditions de température et de pression données.
= m/V avec m: masse (kg) et V: volume (m^3)
La densité d d’une espèce chimique est le rapport de
la masse volumique de cette espèce sur la masse
volumique d’un corps de référence. La densité n’a
donc pas d’unité.
d = (eau) Avec (eau) = 1,00 kg/L = 1,00g/L
Identification d'une espèce chimique:
La chromatographie est une technique d’analyse basée
sur la séparation de différents corps purs constituant
un mélange
Pour réaliser une CCM on utilise un support constitué
d’une couche mince de matériau absorbant (exemple :
plaque silice) et un éluant qui entraîne les différents
constituants du mélange.
La plaque obtenue à la fin s’appelle un
chromatogramme .
I- Lire la notice d'un médicament
Un médicament peut exister sous plusieurs
formes (cachet, gélule, poudre, sirop,
spray, …), c’est la forme galénique du
médicament, il se compose de deux types
de substances :
-Le principe actif dont l’intérêt
thérapeutique a été démontré.
-Les excipients , qui sont des substances
sans intérêt thérapeutique, mais
incorporés au médicament pour faciliter
l’administration, la conservation ou
l’absorption par l’organisme.
Un médicament princeps (ou
médicament de référence) est un
médicament mis au point par un
laboratoire, qui en garde l’exclusivité
durant les 20 ans qui précède le
passage dans le domaine public de
leur brevet, dès lors d’autres
laboratoires peuvent produire des
médicaments génériques contenant
la même substance active mais des
excipients différents.
Chapitre I : Diagnostic médical
I- Signaux périodiques
Un phénomène périodique est un phénomène qui se répète identique à lui-même
au bout d’un certain temps, souvent noté T appelé période.
La période, notée T ,est le temps au bout du quel un phénomène se
reproduit identique à lui-même, on dit souvent qu’au bout d’une période le
système effectue un cycle. L’unité de la période est la seconde
La fréquence, notée f, est le nombre de cycles effectués par unité de temps, f est
exprimée en Hertz (HZ) ainsi un hertz représente 1 cycle par seconde
La fréquence est l’inverse de la période : f = 1/T
II- Ondes sonores et ondes électromagnétiques
Une onde est la propagation d’une perturbation sans transport de matière
Une onde sonore est un phénomène périodique qui se propage par une
suite de compressions et de dilatations du milieu de propagation.
Elle nécessite un support matériel et ne se propage donc pas dans le vide.
Dans l’air, la vitesse v des ondes sonores et ultrasonores est voisine de
340m/s. Son expression est :
v = d/t
Exemp le d'application médicale l'écographie
Une onde électromagnétique est un signal périodique qui, suivant sa
fréquence (ou sa longueur d’onde), peut être une onde radio, de la lumière
visible, des rayons X etc …
Elle peut se propager sans support matériel, donc dans le vide.
Dans un milieu transparent comme l’air ou le verre la lumière se propage
de façon rectiligne.
La vitesse de la lumière dans l’air est sensiblement égale à celle dans le
vide: c = 3,00 . 108 m/s avec trois chiffres significatifs. Cette célérité
(vitesse) a pour expression :
c = d/t
Exemple d'application médicale: les rayons X