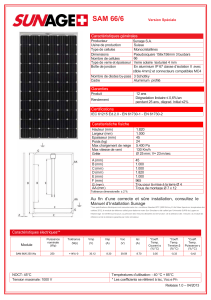
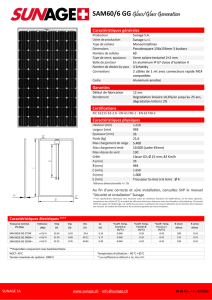
Télécharger

Exercices autour du CM 3 (Modèles linéaires
gaussiennes)
SB & RR
28 septembre 2015
Contents
1 Données synthétiques 1
1.1 Traitement des données synthétiques à la main . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Traitement des données synthétiques à l’aide de lm ........................ 2
1.3 Comparaison des régions de confiance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.4 Estimation de la variance du bruit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2 Sélection de modèles (données synthétiques) 3
3 Données whiteside 4
3.1 Séparation des données en deux sous-échantillons, régression linéaire sur les deux sous-échantillons. 5
3.2 Faire réaliser l’approche split-apply-combine par lm mais en créant les variables de contraste
àlamain ............................................... 7
3.3 Testd’hypothèsesassocié. ...................................... 9
3.4 Variantes ............................................... 9
3.5 Visualiser ............................................... 11
3.6 Lesoutilsdediagnostic ....................................... 13
3.7 Elimination de quelques points suspects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1 Données synthétiques
On veut d’abord travailler sur un problème de régression gaussienne dont on aura choisi la matrice de design
“au hasard” en effectuant des tirages gaussiens.
n<-100
p<-10
sigma <- 1
Créer une matrice Zde dimensions n×p.
Z <- matrix(rnorm(n*p), ncol=p)
On pourra étudier la décomposition spectrale de ZtZà l’aide de eigen ou appliquer à Zla fonction svd.
Choisir θet engendrer le bruit. On choisit θau hasard en effectuant des tirages exponentiels.
1

theta <- rexp(p)
eps <- rnorm(n)
Y <- Z %*% theta + eps
1.1 Traitement des données synthétiques à la main
Estimation par la méthode des moindres carrés. Utiliser (par exemple) la fonction solve.
#thetahat <- .... #
#Yhat <- ... # predictions
#residuals <- ... # residus
cov(residuals,Yhat)
Spectre de ZtZ.
Calcul de Residual Sum of Squares
Visualiser prédictions Yhat contre valeurs de Y
1.2 Traitement des données synthétiques à l’aide de lm
On essaye maintenant de traiter les données synthétiques à l’aide de la fonction lm . Pour cela il faut d’abord
mettre les données synthétiques sous forme de data.frame . On crée un data.frame avec n lignes et p + 1
colonnes (les pvariables explicatives et la variable à expliquer).
df <- as.data.frame(cbind(Y,Z))
names(df) <- c("Y", plyr::aaply(.data=1:10,.margin=1,.fun= function(n) paste("x",n,sep="")))
On peut maintenant évoquer lm.
Essayer deux formulae :Y ~ . -1 et Y~.. Quelles différences ?
#lm0 <- ...
#summary(lm0)
Visualiser à nouveau résidus contre prédictions (on les retrouve comme attributs de “lm0)
#ggplot2::qplot(...)
1.3 Comparaison des régions de confiance
Lorsque la variance du buit homoscédastique est connue, l’ellipsoïde de confiance est construit à partir des
quantiles de la loi du χ2.
Lorsque la variance n’est pas connue, l’ellipsoïde de confiance est construit à partir des quantiles de la loi de
Fischer.
1.4 Estimation de la variance du bruit
Estimation de σ.
2

# sigmahat2 <- ...
Region de confiance pour σ2et pour les prédictions
alpha <- .05
# sum((Y-Yhat)^2)*c(1/qchisq(1-alpha/2,df = n-p),1/qchisq(alpha/2,df=n-p))
2 Sélection de modèles (données synthétiques)
On construit maintenant un paramètre en imposant la nullité de quelques colonnes 1, . . . , k
k<-5
theta <- c(rep(0,5),rexp(p-k))
Y <- Z %*% theta + eps
df <- as.data.frame(cbind(Y,Z))
names(df) <- c("Y", plyr::aaply(.data=1:10,.margin=1,.fun= function(n) paste("x",n,sep="")))
lm10 <- lm(formula = Y~.,data = df)
summary(lm10)
##
## Call:
## lm(formula = Y ~ ., data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.91945 -0.62654 0.05619 0.60252 2.40351
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.22026 0.10694 2.060 0.0424 *
## x1 0.18977 0.09776 1.941 0.0554 .
## x2 -0.13897 0.11003 -1.263 0.2099
## x3 -0.14603 0.09993 -1.461 0.1474
## x4 -0.11199 0.09255 -1.210 0.2295
## x5 -0.05328 0.10720 -0.497 0.6204
## x6 0.20529 0.10215 2.010 0.0475 *
## x7 0.72875 0.11237 6.485 4.83e-09 ***
## x8 0.59010 0.10646 5.543 3.00e-07 ***
## x9 3.47499 0.09708 35.793 < 2e-16 ***
## x10 1.47221 0.08392 17.544 < 2e-16 ***
## ---
## Signif. codes: 0 '***'0.001 '**'0.01 '*'0.05 '.'0.1 ' ' 1
##
## Residual standard error: 0.9589 on 89 degrees of freedom
## Multiple R-squared: 0.9422, Adjusted R-squared: 0.9357
## F-statistic: 145.1 on 10 and 89 DF, p-value: < 2.2e-16
3

xtable::xtable(summary(lm10))
% latex table generated in R 3.2.1 by xtable 1.7-4 package % Mon Oct 5 08:55:47 2015
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.2203 0.1069 2.06 0.0424
x1 0.1898 0.0978 1.94 0.0554
x2 -0.1390 0.1100 -1.26 0.2099
x3 -0.1460 0.0999 -1.46 0.1474
x4 -0.1120 0.0926 -1.21 0.2295
x5 -0.0533 0.1072 -0.50 0.6204
x6 0.2053 0.1022 2.01 0.0475
x7 0.7288 0.1124 6.49 0.0000
x8 0.5901 0.1065 5.54 0.0000
x9 3.4750 0.0971 35.79 0.0000
x10 1.4722 0.0839 17.54 0.0000
Recalcul du modèle en imposant la nullité des premiers coefficients : quand s’arrêter ?
lm_2_10 <- update(object=fit, . ~ . - x1)
xtable::xtable(summary(lm_2_10))
lm_3_10 <- update(object=lm_2_10, . ~ . - x2)
xtable::xtable(summary(lm_3_10))
lm_4_10 <- update(object=lm_3_10, . ~ . - x3)
xtable::xtable(summary(lm_4_10))
lm_5_10 <- update(object=lm_4_10, . ~ . - x4)
xtable::xtable(summary(lm_5_10))
lm_6_10 <- update(object=lm_5_10, . ~ . - x5)
xtable::xtable(summary(lm_6_10))
lm_7_10 <- update(object=lm_6_10, . ~ . - x6)
xtable::xtable(summary(lm_7_10))
lm_8_10 <- update(object=lm_7_10, . ~ . - x7)
xtable::xtable(summary(lm_8_10))
xtable::xtable(summary(lm_8_10))
Où en sommes nous ?
getCall(lm_8_10)
3 Données whiteside
Les données whiteside sont issues du package MASS
data(whiteside, package = 'MASS')
head(whiteside)
## Insul Temp Gas
## 1 Before -0.8 7.2
## 2 Before -0.7 6.9
4

## 3 Before 0.4 6.4
## 4 Before 2.5 6.0
## 5 Before 2.9 5.8
## 6 Before 3.2 5.8
?whiteside
Effectuer une régression de Gas par rapport à Temp.
lm1 <- lm(data=whiteside, formula = Gas ~ Temp )
Visualiser Gas contre Temp en utilisant un code forme ou couleur pour la variable qualitative Insul .
ggplot2::ggplot(data=whiteside) +
ggplot2::geom_point(mapping=ggplot2::aes(...))+
ggplot2::geom_abline(intercept=...,slope=...)
On observe que les points correspandant à l’hiver précédent l’isolation se situent au dessus de la droite de
régression et les autres au dessous. Si on postule une dépendance linéaire entre Temp et Gas , on peut se
demander si l’isolation modifie les paramètres de cette liaison.
Avant de ce lancer dans l’étude de cette liaison, on peut chercher à comparer les deux hivers.
xtable::xtable(dplyr::group_by(.data=whiteside,Insul) %>% dplyr::summarise(mean(Temp),sd(Temp)))
% latex table generated in R 3.2.1 by xtable 1.7-4 package % Mon Oct 5 08:55:47 2015
Insul mean(Temp) sd(Temp)
1 Before 5.35 2.87
2 After 4.46 2.62
Peut-on déceler l’effet du réchauffement climatique ?
ggplot2::qplot(data=whiteside, y= Temp, x=Insul, geom="boxplot")
L’hiver qui suit l’isolation semble plus doux que l’hiver précédent. Il n’est donc pas loyal de chercher à
comparer les consommations de gaz globalement. Il faut essayer de comparer ces consommations de gaz
toutes choses égales par ailleurs.
3.1 Séparation des données en deux sous-échantillons, régression linéaire sur
les deux sous-échantillons.
lm2 <- dplyr::filter(.data=whiteside, Insul=='Before') %>% lm(formula = Gas ~ Temp)
lm3 <- dplyr::filter(.data=whiteside, Insul=='After') %>% lm(formula = Gas ~ Temp)
ou alors d’une pierre deux coups . . .
by(whiteside,INDICES = whiteside$Insul, FUN=lm, formula = Gas ~Temp)
5