Radioactivité e..

Dr A. Sicard CapeSup Grenoble Page 1
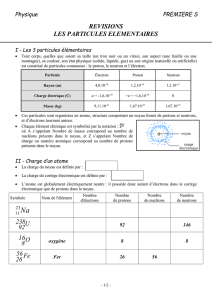
Cours n°11 : Radioactivité et nucléaire
1) Le noyau atomique
1.1) Structure
1.1.1) Structure de la matière
La matière est constituée de molécules ou d’atomes pour les corps simples.
Ces molécules sont elles-mêmes constituées d’atomes, atomes étant formés d’un noyau central
entouré d’un nuage électronique.
Structure de l’atome
L’atome est formé d’un nuage électronique entourant un noyau central.
Chaque électron porte la charge négative
==1,6022 1019
Du fait de la neutralité de l’atome, le noyau est chargé positivement d’une charge égale et opposée
en signe à celle du nuage électronique.
Structure du noyau
Le noyau atomique est composé de particules appelées nucléons. Ceux-ci se répartissent en protons
et neutrons. Les protons sont des particules chargées positivement avec la charge élémentaire
== 1,6022 1019
Les neutrons sont des particules portant une charge neutre.
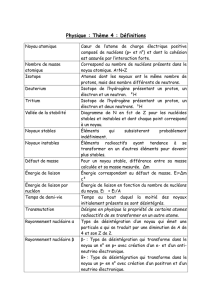
1.1.2) Définitions
Elément chimique
Un élément chimique est l’ensemble des atomes ou ions monoatomiques ayant le même nombre de
protons dans leur noyau.
On écrit :
est le symbole de l’élément
= nombre de protons = numéro atomique = nombre de charge
Exemples
6
: élément carbone
8
: élément oxygène

Dr A. Sicard CapeSup Grenoble Page 2
Nucléide
L’ensemble des noyaux qui possèdent le même nombre de protons et le même nombre de neutrons
est appelé un nucléide. Un nucléide est noté :
est le symbole de l’élément
= nombre de protons ou nombre de charge
= nombre de nucléons ou nombre de charge
Le nombre de neutrons est donné par = .
Exemple :
8
16
Elément oxygène
Nombre de protons = 8
Nombre de nucléons =16
Nombre de neutrons == 8
Nom du nucléide Oxygène 16
Deux nucléides sont dits isotopes s’ils ont même nombre de protons .
Exemple :
6
12 (carbone 12) et
6
14 (carbone 14).
Pour un élément donné, on définit l’abondance isotopique ou abondance naturelle de chaque
isotope par son pourcentage en masse dans un mélange naturel de cet élément.
Deux nucléides sont dits isobares s’ils ont même nombre de nucléons .
Deux nucléides sont dits isotones s’ils ont même nombre de neutrons
Aide mémoire :
- isotoNe : neutrons
6
13 carbone 13 et
7
14 azote 14
- isotoPe : protons
6
12 carbone 12 et
6
14 carbone 14
- isobAre : nombre de masse (nucléons)
6
14 carbone 14 et
7
14 azote 14
1.1.3) Masse
Convention
Pour un nucléide donné
, on note :
()= masse du noyau
()= masse de l’atome
()= masse molaire atomique

Dr A. Sicard CapeSup Grenoble Page 3
On a les relations suivantes ()()
et ()= ()
Unité de masse atomique
Pour travailler à l’échelle de l’atome, le kilogramme n’est pas adapté. On définit pour cela l’unité de
masse atomique.
L’unité de masse atomique de symbole ... ou est égale au douzième de la masse de l’atome
de carbone 12. On a :
1 =1
12 (
6
12 )
1 = 1,6605402 1027
Masse du noyau
Avec la définition de l’unité de masse atomique, on peut écrire la masse des nucléons :
- proton : = 1,6726 1027 = 1,00728
- neutron : = 1,6749 1027 = 1,00866
1 et
(en )
= 9,1093 1031 = 5,5 104
Masse molaire atomique
Une mole d’éléments correspond à la quantité de matière constituée de éléments où est la
constante d’Avogadro de valeur : = 6,022 1023 1
La masse molaire atomique de l’atome
est la masse d’un échantillon constitué d’une mole
d’atomes
.
=
On a :
en
1.1.4) Energie
Pour travailler à l’échelle atomique, le joule n’est pas adapté. On préférera l’électronvolt.
Un électronvolt (1 ) est défini comme l’énergie acquise par un électron sous une différence de
potentiel de 1 .
1 = 1,6022 1019 = en

Dr A. Sicard CapeSup Grenoble Page 4
1.2) Stabilité du noyau
1.2.1) Equivalence masse-énergie
En 1905, en élaborant la théorie de la relativité restreinte, Einstein postula l’équivalence masse-
énergie. Il avait alors 26 ans.
Tout corps, même au repos, possède du seul fait de sa masse une énergie appelée énergie de
masse.
= 2
: énergie de masse ()
: masse ()
= 3 108 1 : vitesse de la lumière dans le vide
Ainsi, un système qui échange une quantité d’énergie avec le système extérieur subit une
variation de masse telle que :
=
2
1.2.2) Défaut de masse du noyau
La masse d’un noyau est inférieure à la somme des masses de ses nucléons pris séparément. C’est ce
que l’on appelle le défaut de masse.
Le défaut de masse, positif, est la différence entre la somme des masses des ses nucléons pris
séparément et la masse de ce noyau.
Il s’exprime pour un noyau
par la quantité telle que :
= +()
1.2.3) Energie de liaison
On appelle énergie de liaison l’énergie qu’il faut fournir à un noyau au repos pour le dissocier en ses
nucléons au repos. Elle s’exprime en fonction du défaut de masse comme :
= 2
L’énergie de liaison correspond à l’énergie mise en jeu par l’ensemble des nucléons constitutifs du
noyau pour assurer sa stabilité.
L’énergie de liaison est égale à la différence entre la somme des énergies de masse des nucléons
séparés et l’énergie de masse du noyau. Elle correspond également à l’énergie récupérée lors de la
formation d’un noyau à partir de ses nucléons dissociés.

Dr A. Sicard CapeSup Grenoble Page 5
Exemple : calcul de l’énergie de liaison d’un noyau d’hélium 4
2
4
Données : (
2
4)= 4,0015
= 1,00728
= 1,00866
Calcul du défaut de masse
= 2 +(42) (
2
4)
= 2 × 1,00728 + 2 × 1,00866 4,0015
= 0,0304
Simplification de calcul :
=931,5 × 0,0304 =28,3
Energie de liaison par nucléon :
Afin de pouvoir comparer la stabilité des différents nucléides les uns par rapport aux autres, on
définit l’énergie de liaison par nucléon comme :
Avec l’énergie de liaison et le nombre de nucléons du nucléide.
Un noyau est d’autant plus stable que son énergie de liaison moyenne par nucléon est grande.
On représente la courbe d’Aston donnant
en fonction de .
nucléons séparés
noyau
énergie de
masse
Défaut de masse en
Energie de liaison en
×931,5
/ 931,5
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
1
/
13
100%