Correction du devoir maison n° 1

Correction du DM n ° 1 : Exercices à propos de l'œil
Exercice 1 :
1. La distance focale f' est la distance algébrique (centre optique - point où converge un faisceau de rayons
parallèles à l'axe optique) dans le cas d'une lentille convergente ou d'où semblent provenir les rayons d'un
faisceau de rayons parallèles à l'axe optique dans le cas d'une lentille divergente.
C =
'
1
OF
, la vergence est l'inverse de la distance focale :
Avec C en dioptrie (δ) et f' =
'OF
en mètre (m). C > 0 si la lentille est convergente et < 0 si la lentille est
divergente.
2.a. L'utilisation de la formule de conjugaison nous permet d'obtenir la valeur de
'OA
et donc la position de
l'image, celle de la formule du grandissement nous permet alors de déterminer la taille de cette image. Nous
obtenons :
'OA
= 24 cm et
'' BA
= -2 cm. L'image est donc réelle et inversée.
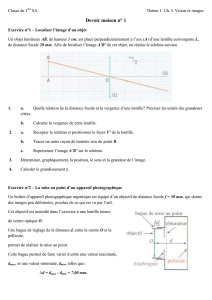
b. Voir schéma 1 dans le classeur.
3.a. Nous réutilisons les mêmes formules (mais avec f' < 0) et obtenons
'OA
= - 4,8 cm (l'image est virtuelle)
et
'' BA
= 0,4 cm (elle est droite (non renversée)).
b. Voir schéma 2 dans le classeur.
4.a. Pour déterminer la position de l'image par ce système optique, il faut cette fois-ci appliquer par deux fois
la relation de conjugaison. La première fois (relation de conjugaison pour la lentille L1) nous redonne les
résultats du 2.a. :
'
1AO
= 24 cm. Nous en déduisons donc que
'
2AO
=
12OO
+
'
1AO
= -20 + 24 = 4 cm et
pouvons ensuite appliquer la relation de conjugaison à la lentille L2. Nous obtenons alors
"
2AO
= 8 cm.
L'image est donc réelle.
Pour déterminer la taille de cette image, il faut appliquer par deux fois la formule du grandissement. La
première application (pour la lentille L1) nous donne le résultat du 2.a.
'' BA
= -2 cm. La deuxième
application (pour la lentille L2) nous donne
"" BA
= 2
'' BA
= - 4 cm. L'image est donc inversée.
b. Voir schéma 3 dans le classeur.
Exercice 2 :
1. Le Punctum Proximum est proche et le Punctum Remotum peu éloigné, il s'agit donc d'un œil myope.
2.a. Cas de l'œil accommodant au maximum : Au Punctum Proximum , l'objet est placé à une distance
OA
= - 8,5 cm. En considèrant que
'OA
= 16 mm = 1,6 cm (distance cristallin-rétine), il est loisible
d'appliquer la formule de conjugaison : 1/1,6.10-2 - (-1/8,5.10-2) = 1/
'OF
. Le résultat obtenu est alors :
'OF
= 13,5 mm = 1,35 cm.
b. Dans le cas de l'œil n'accommodant pas : Au Punctum Remotum, l'objet est placé à une distance
OA
= -21 cm, le même type de raisonnement (nous avons toujours
'OA
= 16 mm) nous conduit à
'OF
= 15 mm = 1,5 cm.
Nous pouvons donc écrire : 13,5 mm < f' < 15 mm
3.a. Deux raisonnements sont possibles :
Il faut que la lentille corrige le défaut de l'œil myope, trop convergent. C'est donc une lentille
divergente dont la vergence est telle que la somme des vergences de l'œil myope au repos (OMR)
et de la lentille donne la vergence d'un œil normal au repos (L'image d'un objet à l'infini devant se
former sur la rétine donc C = 1/f', où f' = 16 mm) : Cdiv + COMR = 1/1,6.10-2. Comme COMR = 1/
'OF
et que
'OF
a été calculé au 2.b., nous obtenons : Cdiv = 62,5 - 67,2 = - 4,7 δ. Sa distance focale est
donc f'div = 1/Cdiv = -21 cm.
L'objet à l'infini doit, pour être vu sans accommodation par l'œil myope, donner, après traversée
de la lentille, une image au Punctum Remotum de l'œil myope soit à - 21 cm de l'œil et donc à -

20 cm de la lentille (située à 1 cm de l'œil). Le foyer image de la lentille est donc à -20 cm de son
centre, soit une distance focale f'div = 20 cm et une vergence de Cdiv = 1/0,2 = 5 δ.
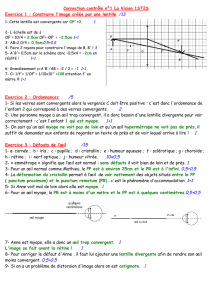
b. Voir schéma 4 dans le classeur.
c. La distance minimale de vision nette correspond à l'œil accomodant au maximum (OMA). Nous avons
calculé au 2.a. que la vergence de cet œil est alors de COMA = 74,24 δ. La vergence de cet œil corrigé (OMC)
par la lentille divergente est donc : COMC = COMA + Cdiv = 74,2 - 5 = 69,2 δ. L'application de la formule de
conjugaison nous donne (avec
'OA
= 1,6.10-3 m et 1/
'OF
= COMC = 69,2 δ),
OA
= - 0,143 m = -14,3 cm. La
vision minimale distincte est donc passé de 8,5 à 14,3 cm.
d. Voir schéma 5 dans le classeur.
4. La presbytie repousse le Punctum Proximum un peu plus loin par fatigue des muscles du cristallin
a. Les mêmes calculs qu'en 2.a. et 2.b. nous donne : 14,5 mm < f' < 15 mm.
b. En prenant l'inverse de l'encadrement obtenu au a., nous obtenons : 67,25 < COP < 69 (avec COP la
vergence de l'œil presbyte) soit après correction 67,2 - 4,7 = 62,5 < COPC < 69 - 4,7 = 64,3. L'application
de la formule de conjugaison pour ces deux valeurs extrêmes nous donne -0,66 <
OA
< - ∞ soit une
vision nette entre 66 cm et l'infini.
5. Ici aussi, deux raisonnements sont possibles :
L'œil au repos corrigé de ces deux lentilles doit donner d'un objet à 31 cm une image nette à 1,6
cm. La relation de conjugaison nous donne donc CO2C = 65,7 δ. Or CO2C = COMR + C1 + C2 d'où on
tire C2 = 3,2 δ et donc f'2 = 1/3,2 = 0,31 = 31 cm.
L'œil corrigé voit sans accomoder un objet à l'infini. La lentille L2 doit donc donner de l'objet à -
31 cm une image à - ∞. La relation de conjugaison donne donc 1/
'OF
= 1/0,31 (puisque 1/
'OA
=
0). Soit f'1 = 31 cm et C1 = 3,2 δ.
Exercice 3 :
Voir schéma 6 dans le classeur.
1. Pour un œil normal, un objet situé à 200 mètres est considéré comme étant à l'infini. Il donne, sans
accomodation, une image dans le plan focal, c'est-à-dire sur la rétine. La formule du grandissement nous
donne alors 200/0,016 = 1,60/
'' BA
d'où
'' BA
= 1,28.10-4 m = 128 µm.
2.a. Le pouvoir séparateur ou acuité visuelle est égal à α = 4,5.10-6/1,6.10-2 = 2,8.10-4 rad. N'oublions pas en
effet que pour de petits angles, on peut approximer la tangente à la valeur de l'angle pourvu qu'il soit
exprimer en radian.
b. La distance minimale entre deux points séparés par l'œil et situés à 25 cm de lui est donnée par :
AB
=
'' BA
× D/f' = 4,5.10-6 × 0,25 / 1,6.10-2 = 7.10-5 m
ou
AB
= α × D = 2,8.10-4 × 0,25 = 7.10-5 m.
c. Deux solutions également :
Calcul de
'' BA
= f' ×
AB
/ D = 1,6.10-2 × 1,2 / 5000 = 3,84.10-6 m < 4,5.10-6 m (taille d'une
cellule photosensible). Les deux points ne seront pas séparés.
Calcul de l'angle sous lequel on voit les phares de la voiture noté β :
β =
AB
/ D = 1,2 / 5000 = 2,4.10-4 rad < 2,8.10-4 rad (α : acuité visuelle). Les deux points ne
seront pas séparés.
3. Voir schéma 7 dans le classeur.
La distance
MIN
AB
pour un œil myope dont le Punctum Proximum est donnée comme dans le 2.b. par
AB
=
'' BA
× D/f' où
'' BA
est toujours la taille d'une cellule photosensible (4,5.10-6 m), f' toujours égale à 16 mm
(soit 1,6.10-2 m) mais où D ne vaut que 8.10-2 m. On en déduit
MIN
AB
= 2,25.10–5 m.
Avec ses lunettes, une personne myope recouvre une vue presque normale et donc un Punctum Proximum de
plus de 14 cm (voir exercice 2) soit une distance
MIN
AB
de près de 40 µm alors que sans ses lunettes, il
divise d'un facteur deux cette distance.